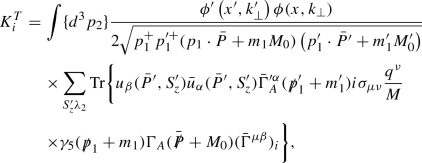Abstract
The transition form factors for doubly heavy baryons into a spin-1/2 or spin-3/2 ground-state baryon induced by both the charged current and the flavor changing neutral current are systematically studied within the light-front quark model. In the transition the two spectator quarks have two spin configurations and both are considered in this calculation. We use an updated vertex functions, and inspired by the flavor SU(3) symmetry, we also provide a new approach to derive the flavor-spin factors. With the obtained transition form factors, we perform a phenomenological study of the corresponding semi-leptonic decays of doubly heavy baryons induced by the \(c\rightarrow d/s \ell ^+\nu \), \(b\rightarrow c/u\ell ^-\bar{\nu }\) and \(b\rightarrow d/s\ell ^+\ell ^-\). Results for partial decay widths, branching ratios and the polarization ratios \(\Gamma _{L}/\Gamma _{T}\)s are given. We find that most branching ratios for the semi-leptonic decays induced by the \(c\rightarrow d,s\) transitions are at the order of \(10^{-3}\sim 10^{-2}\), which might be useful for the search of other doubly-heavy baryons. Uncertainties in form factors, the flavor SU(3) symmetry and sources of symmetry breaking effects are discussed. We find that the SU(3) symmetry breaking effects could be sizable in charmed baryon decays while in the bottomed case, the SU(3) symmetry breaking effects are less significant. Our results can be examined at the experimental facilities in the future.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In hadron physics, quark model has become a well-established tool for the classification of various hadronic states. Most predictions of the quark model have already been experimentally confirmed, but the quest for doubly heavy baryons, baryonic states made of two heavy charm/bottom quarks, has been conducted for a long time. These baryonic states had never been observed in experiments until 2017, when the LHCb collaboration announced the discovery of \(\Xi _{cc}^{++}\) via \(\Xi _{cc}^{++} \rightarrow \Lambda _c^{+} K^- \pi ^+ \pi ^+\) [1] with the decay mode suggested in Ref. [2]. This discovery is subsequently confirmed in 2018 in the \(\Xi _{cc}^{++} \rightarrow \Xi _c^+ \pi ^+\) decay [3], and meanwhile triggered a series of experimental investigations [4,5,6,7]. Now studies of doubly-heavy baryons now open a window to study the hadron spectroscopy and strong interactions in a baryonic system in the presence of two heavy constituent quarks.
Among various properties on doubly heavy baryons, weak decays are of special importance. In the experimental searches for new type of particles the firstly-discovered ones are usually the ground states, which can only be reconstructed via weak decay final states. Thus theoretical analysis of their weak decays can greatly help to optimize the experimental resources. Meanwhile, there exists rich dynamics in weak decay processes and currently only few theoretical approaches are available, which makes them a wonderland full of challenges and opportunities.
On the theoretical side an ingredient in the weak decay is the transition matrix element of the parent particle to a daughter particle, which can be parameterized as form factors. Fortunately, there are various available methods for this part of transition on the market. Thus the decays of a doubly heavy baryon to a singly heavy baryon transition are studied intensively [2, 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. In particular, some of the form factors are studied under the light-front quark model (LFQM) [8, 13, 22, 25], QCD sum rules [26] and light cone sum rules [27, 28].
The LFQM is originally developed in meson decays [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. During the last decade it was applied to baryon decays with the help of quark-diquark picture [50,51,52,53,54], and it is also interesting to notice that Ref. [25] has adopted the three-quark transition for the form factors. Under the quark-diquark picture, the two spectator quarks play the role of the antiquark in a mesonic system and are treated as a system of spin-0 or 1. In the calculation the vertex functions are associated with the couplings of a baryon to its quark and diquark constituents. Following a recent work [55] we revise the vertex function concerned with the spin-1 diquark system in this paper, and consequently we update the form factors of a doubly heavy baryon to a singly heavy baryon transitions under the LFQM. As argued in a previous work [13], both spin-1/2 to spin-1/2 and spin-1/2 to spin-3/2 transitions are important to the potential discovery channels, and thus both transitions are studied in this work. Meanwhile, we investigate the transitions induced by charged current as well as the ones induced by flavor changing neutral current (FCNC). To be more specific, we will explore the following transitions:
- 1.
the spin-1/2 to spin-1/2 transition with the charged current,Footnote 1
\(c\rightarrow d,s\) processes,
$$\begin{aligned}&\left. \begin{array}{lcl} \Xi _{cc}^{++}(ccu) &{} \rightarrow &{}\Lambda _{c}^{+}(dcu)/\Sigma _{c}^{+}(dcu)/\Xi _{c}^{(\prime )+}(scu),\\ \Xi _{cc}^{+}(ccd) &{} \rightarrow &{}\Sigma _{c}^{0}(dcd)/\Xi _{c}^{0}(scd)/\Xi _{c}^{\prime 0}(scd),\\ \Omega _{cc}^{+}(ccs) &{} \rightarrow &{}\Xi _{c}^{0}(dcs)/\Xi _{c}^{\prime 0}(dcs)/\Omega _{c}^{0}(scs), \end{array} \right. \\&\quad \left. \begin{array}{lcl} \Xi _{bc}^{+}/\Xi _{bc}^{\prime +}(cbu) &{} \rightarrow &{}\Lambda _{b}^{0}(dbu)/\Sigma _{b}^{0}(dbu)/\Xi _{b}^{(\prime )0}(sbu),\\ \Xi _{bc}^{0}/\Xi _{bc}^{\prime 0}(cbd) &{} \rightarrow &{}\Sigma _{b}^{-}(dbd)/\Xi _{b}^{-}( sbd)/\Xi _{b}^{\prime -}(sbd),\\ \Omega _{bc}^{0}/\Omega _{bc}^ {\prime 0}(cbs) &{} \rightarrow &{}\Xi _{b}^{-}(dbs)/\Xi _{b}^{\prime -}(dbs)/\Omega _{b}^{-}(sbs); \end{array} \right. \end{aligned}$$\(b\rightarrow u,c\) processes,
$$\begin{aligned}&\left. \begin{array}{lcl} \Xi _{bb}^{0}(bbu) &{} \rightarrow &{}\Sigma _{b}^{+}(ubu)/\Xi _{bc}^{+}(cbu)/\Xi _{bc}^{\prime +}(cbu),\\ \Xi _{bb}^{-}(bbd) &{} \rightarrow &{}\Lambda _{b}^{0}(ubd)/\Sigma _{b}^{0} (ubd)/\Xi _{bc}^{0}(cbd)/\Xi _{bc}^{\prime 0}(cbd),\\ \Omega _{bb}^{-}(bbs) &{} \rightarrow &{}\Xi _{b}^{0}(ubs)/\Xi _{b}^{\prime 0}(ubs) /\Omega _{bc}^{0}(cbs)/\Omega _{bc}^{\prime 0}(cbs), \end{array} \right. \\&\quad \left. \begin{array}{lcl} \Xi _{bc}^{+}/\Xi _{bc}^{\prime +}(bcu) &{} \rightarrow &{}\Sigma _{c}^{++}(ucu)/\Xi _{cc}^{++}(ccu),\\ \Xi _{bc}^{0}/\Xi _{bc}^{\prime 0}(bcd) &{} \rightarrow &{}\Lambda _{c}^{+}(ucd)/\Sigma _{c}^{+}(ucd)/\Xi _{cc}^{+}(ccd),\\ \Omega _{bc}^{0}/\Omega _{bc}^{\prime 0}(bcs) &{} \rightarrow &{}\Xi _{c}^{+}(ucs)/\Xi _{c}^{\prime +}(ucs)/\Omega _{cc}^{+}(ccs); \end{array} \right. \end{aligned}$$
- 2.
the \({1}/{2}\rightarrow {1}/{2}\) transition with FCNC,
\(c\rightarrow u\) processes,
$$\begin{aligned}&\left. \begin{array}{lcl} \Xi _{cc}^{++}(ccu) &{} \rightarrow &{}\Sigma _{c}^{++}(ucu),\\ \Xi _{cc}^{+}(ccd) &{} \rightarrow &{}\Lambda _{c}^{+}(ucd)/\Sigma _{c}^{+}(ucd),\\ \Omega _{cc}^{+}(ccs) &{} \rightarrow &{}\Xi _{c}^{+}(ucs)/\Xi _{c}^{\prime +}(ucs), \end{array} \right. \\&\quad \left. \begin{array}{lcl} \Xi _{cb}^{+}/\Xi _{cb}^{\prime +}(cbu) &{} \rightarrow &{} \Sigma _{b}^{+}(ubu),\\ \Xi _{cb}^{0}/\Xi _{cb}^{\prime 0}(cbd) &{} \rightarrow &{} \Lambda _{b}^{0}(ubd)/\Sigma _{b}^{0}(ubd),\\ \Omega _{cb}^{0}/\Omega _{cb}^{\prime 0}(cbs) &{} \rightarrow &{}\Xi _{b}^{0}(ubs)/\Xi _{b}^{\prime 0}(ubs); \end{array} \right. \end{aligned}$$
\(b\rightarrow d,s\) processes,
$$\begin{aligned}&\left. \begin{array}{lcl} \Xi _{bb}^{0}(bbu) &{} \rightarrow &{}\Lambda _{b}^{0}(dbu) /\Sigma _{b}^{0}(dbu)/\Xi _{b}^{(\prime )0}(sbu),\\ \Xi _{bb}^{-}(bbd) &{} \rightarrow &{}\Sigma _{b}^{-}(dbd)/\Xi _{b}^{-}(sbd)/\Xi _{b}^{\prime -}(sbd),\\ \Omega _{bb}^{-}(bbs) &{} \rightarrow &{}\Xi _{b}^{-}(dbs)/\Xi _{b}^{\prime -}(dbs)/\Omega _{b}^{-}(sbs), \end{array} \right. \\&\quad \left. \begin{array}{lcl} \Xi _{bc}^{+}/\Xi _{bc}^{\prime +}(bcu) &{} \rightarrow &{}\Lambda _{c}^{+}(dcu)/\Sigma _{c}^{+}(dcu)/\Xi _{c}^{(\prime )+}(scu),\\ \Xi _{bc}^{0}/\Xi _{bc}^{\prime 0}(bcd) &{} \rightarrow &{}\Sigma _{c}^{0}(dcd)/\Xi _{c}^{0}(scd)/\Xi _{c}^{\prime 0}(scd),\\ \Omega _{bc}^{0}/\Omega _{bc}^{\prime 0}(bcs) &{} \rightarrow &{}\Xi _{c}^{0}(dcs)/\Xi _{c}^{\prime 0}(dcs)/\Omega _{c}^{0}(scs); \end{array} \right. \end{aligned}$$
- 3.
the \({1}/{2}\rightarrow {3}/{2}\) transition induced by the charged current,
\(c\rightarrow d,s\) processes,
$$\begin{aligned}&\left. \begin{array}{lcl} \Xi _{cc}^{++}(ccu) &{} \rightarrow &{}\Sigma _{c}^{*+}(dcu)/\Xi _{c}^{\prime *+}(scu),\\ \Xi _{cc}^{+}(ccd) &{} \rightarrow &{}\Sigma _{c}^{*0}(dcd)/\Xi _{c}^{\prime *0}(scd),\\ \Omega _{cc}^{+}(ccs) &{} \rightarrow &{}\Xi _{c}^{\prime *0}(dcs)/\Omega _{c}^{*0}(scs), \end{array} \right. \\&\quad \left. \begin{array}{lcl} \Xi _{bc}^{+}/\Xi _{bc}^{\prime +}(cbu) &{} \rightarrow &{}\Sigma _{b}^{*0}(dbu)/\Xi _{b}^{\prime *0}(sbu),\\ \Xi _{bc}^{0}/\Xi _{bc}^{\prime 0}(cbd) &{} \rightarrow &{}\Sigma _{b}^{*-}(dbd)/\Xi _{b}^{\prime *-}(sbd),\\ \Omega _{bc}^{0}/\Omega _{bc}^{\prime 0}(cbs) &{} \rightarrow &{}\Xi _{b}^{\prime *-}(dbs)/\Omega _{b}^{*-}(sbs). \end{array} \right. \end{aligned}$$\(b\rightarrow u,c\) processes,
$$\begin{aligned}&\left. \begin{array}{lcl} \Xi _{bb}^{0}(bbu) &{} \rightarrow &{}\Sigma _{b}^{*+}(ubu)/\Xi _{bc}^{*+}(cbu),\\ \Xi _{bb}^{-}(bbd) &{} \rightarrow &{}\Sigma _{b}^{*0}(ubd)/\Xi _{bc}^{*0}(cbd),\\ \Omega _{bb}^{-}(bbs) &{} \rightarrow &{}\Xi _{b}^{\prime *0}(ubs)/\Omega _{bc}^{*0}(cbs), \end{array} \right. \\&\quad \left. \begin{array}{lcl} \Xi _{bc}^{+}/\Xi _{bc}^{\prime +}(bcu) &{} \rightarrow &{}\Sigma _{c}^{*++}(ucu)/\Xi _{cc}^{*++}(ccu),\\ \Xi _{bc}^{0}/\Xi _{bc}^{\prime 0}(bcd) &{} \rightarrow &{}\Sigma _{c}^{*+}(ucd)/\Xi _{cc}^{*+}(ccd),\\ \Omega _{bc}^{0}/\Omega _{bc}^{\prime 0}(bcs) &{} \rightarrow &{}\Xi _{c}^{\prime *+}(ucs)/\Omega _{cc}^{*+}(ccs); \end{array} \right. \end{aligned}$$
- 4.
the \({1}/{2}\rightarrow {3}/{2}\) transition with FCNC,
\(c\rightarrow u\) processes,
$$\begin{aligned}&\left. \begin{array}{lcl} \Xi _{cc}^{++}(ccu) &{} \rightarrow &{}\Sigma _{c}^{*++}(ucu),\\ \Xi _{cc}^{+}(ccd) &{} \rightarrow &{}\Sigma _{c}^{*+}(ucd),\\ \Omega _{cc}^{+}(ccs) &{} \rightarrow &{}\Xi _{c}^{\prime *+}(ucs), \end{array} \right. \\&\quad \left. \begin{array}{lcl} \Xi _{cb}^{+}/\Xi _{cb}^{\prime +}(cbu) &{} \rightarrow &{} \Sigma _{b}^{*+}(ubu),\\ \Xi _{cb}^{0}/\Xi _{cb}^{\prime 0}(cbd) &{} \rightarrow &{} \Sigma _{b}^{*0}(ubd),\\ \Omega _{cb}^{0}/\Omega _{cb}^{\prime 0}(cbs) &{} \rightarrow &{}\Xi _{b}^{\prime *0}(ubs); \end{array} \right. \end{aligned}$$
\(b\rightarrow d,s\) processes,
$$\begin{aligned}&\left. \begin{array}{lcl} \Xi _{bb}^{0}(bbu) &{} \rightarrow \Sigma _{b}^{*0}(dbu)/\Xi _{b}^{\prime *0}(sbu),\\ \Xi _{bb}^{-}(bbd) &{} \rightarrow \Sigma _{b}^{*-}(dbd)/\Xi _{b}^{\prime *-}(sbd),\\ \Omega _{bb}^{-}(bbs) &{} \rightarrow \Xi _{b}^{\prime *-}(dbs)/\Omega _{b}^{*-}(sbs), \end{array} \right. \\&\quad \left. \begin{array}{lcl} \Xi _{bc}^{+}/\Xi _{bc}^{\prime +}(bcu) &{} \rightarrow \Sigma _{c}^{*+}(dcu)/\Xi _{c}^{\prime *+}(scu),\\ \Xi _{bc}^{0}/\Xi _{bc}^{\prime 0}(bcd) &{} \rightarrow \Sigma _{c}^{*0}(dcd)/\Xi _{c}^{\prime *0}(scd),\\ \Omega _{bc}^{0}/\Omega _{bc}^{\prime 0}(bcs) &{} \rightarrow \Xi _{c}^{\prime *0}(dcs)/\Omega _{c}^{*0}(scs); \end{array} \right. \end{aligned}$$
In the above, the quark components have been explicitly given in the brackets, in which the first quarks denote the quarks participating in the weak decays. The initial baryons are all doubly heavy baryons. The spin-parity \(J^{P}\) quantum numbers of the doubly heavy baryons has been listed in Table 1.
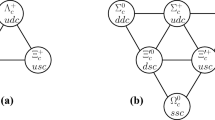
The lowest-lying doubly heavy baryons with \(J^{P}=1/2^{+}\) for example the doubly charm SU(3) triplets \(\Xi _{cc}^{++}\) (ccu), \(\Xi _{cc}^{+}\) (ccd), and \(\Omega ^{+}_{cc}\)(ccs) shown in Fig. 1, can only weak decay. Three doubly bottom baryons \(\Xi _{bb}^{0}\) (bbu), \(\Xi _{bb}^{-}\) (bbd), and \(\Omega ^{-}_{bb}\)(bbs) can also constitute one SU(3) triplet similar to Fig. 1 with the replacement \(c\rightarrow b\). While the bottom-charm baryons could form two sets of SU(3) triplets, (\(\Xi _{bc},\Omega _{bc}\)) and (\(\Xi _{bc}^{\prime },\Omega _{bc}^{\prime }\)). The difference between the two sets is the different total spin of bc system as shown in Table 1, In fact there could be mixing between them. However, the detailed mixing scheme between the two triplets is still unclear, the initial baryons include two triplets, (\(\Xi _{bc},\Omega _{bc}\)) and (\(\Xi _{bc}^{\prime },\Omega _{bc}^{\prime }\)) in this work. The doubly heavy baryons with \(J^{P}=3/2^{+}\) can decay into the lowest-lying ones radiatively if the mass splitting is small, or decay into the lowest-lying ones with the emission of a light pion when they are heavy enough. The final baryons include doubly heavy baryons and singly heavy baryons. The singly heavy baryons can compose one SU(3) anti-triplets \(\varvec{{\bar{3}}}\) and one SU(3) sextet \({\varvec{6}}\) as shown in Fig. 2. Taking the transition \({{\mathcal {B}}}_{bc}\rightarrow {{\mathcal {B}}}_{c}\) with \(b\rightarrow s\) as an example, the final baryons \(\Xi _{c}^{\prime +}\), \(\Xi _{c}^{\prime 0}\) and \(\Omega _{c}^{0}\) belong to the presentation of \({\varvec{6}}\), while \(\Xi _{c}^{+}\) and \(\Xi _{c}^{0}\) are included in the \(\varvec{{\bar{3}}}\), as can be seen from Fig. 2.
Spin-1/2 singly charmed baryons. Here (a) represents SU(3) anti-triplets \(\varvec{{\bar{3}}}\) and (b) represents SU(3) sextets \({\varvec{6}}\). The spin-3/2 singly charmed baryons only have SU(3) sextets \({\varvec{6}}\) as shown by panel (b) just with the replacement “\({{\mathcal {B}}}_{c}\rightarrow \mathcal{B}_{c}^{*}\)”. For spin-1/2 and spin-3/2 singly bottomed baryons, a replacement \(c\rightarrow b\) is needed
This paper is organized as follows. In Sec. II, we will present the framework of the light-front approach under the diquark picture, and then the flavor-spin wave functions will be discussed. In the appendix, we will provide a new approach to derive the flavor-spin factors. Numerical results of various transition form factors are shown in this section. In Sec. III, phenomenological applications of the doubly heavy baryon decays will be carried out, including numerical results of the decay widths, branching ratios and \(\Gamma _{L}/\Gamma _{T}\)s of the semileptonic weak decays of doubly heavy baryons. The SU(3) symmetry breaking effect and error estimations will be also discussed in Sec. III. A brief summary is given in the last section. The appendix also contains some brief description of the flavor-spin wave functions, and helicity amplitudes.
2 Theoretical framework
The theoretical framework for the baryonic transitions induced by charged current and FCNC will be briefly introduced in this section, including the definitions of the states for spin-1/2 and 3/2 baryons, and the extraction of the transition form factors. More details can be found in Refs. [50, 54].
2.1 Light-front quark model
Feynman diagram for doubly heavy baryons B into a spin-1/2 and spin-3/2 ground-state baryons \(B^{\prime }\) with two spectator quarks as a diquark. Here P and \(P^{\prime }\) are the momentum of the initial and final baryons, respectively. In quark level, the transition is one heavy quark \(Q_{1}\) with momentum \(p_{1}\) decays into a lighter quark \(q_{1}\) with momentum \(p_{1}^{\prime }\), and the diquark with momentum \(p_{2}\). The black ball means the weak interaction vertex
For a hadronic state the physical wave functions include the coordinate, color, spin and flavor spaces. Since we will only consider the leading order contribution as shown in Fig. 3, there is no color change between the spectators and quarks attached to the electroweak current, and thus the color dependence is rather simple. We will not write the color dependence explicitly, however we should point out that this is only valid at leading order. Nontrivial color dependence will be introduced at higher orders due to the exchange of colored gluons. The flavor-spin wave functions will be discussed in the second section, with a new derivation method given in the appendices. In this section, we will give the framework by considering the coordinate space wave function, or equivalently the momentum space.
For the \(J^{P}=1/2^{+}\) baryon states, their wave functions in momentum space can be written as
here \(Q_{1}=b,c\) is initial heavy quark, and “\((\mathrm{{di}})\)” presents the diquark shown in Fig. 3. \(\lambda _1\) and \(\lambda _2\) denote their helicities, P is the total momentum of the baryon, \(p_1,~ p_2\) are the on-mass-shell light-front momenta of the heavy quark and the diquark, respectively. In the LFQM, the momentum is defined as \(p=(p^{-},p^{+},p_{\perp })\) with \(p^{\pm }=p^0\pm p^3\) and \(p_{\perp }=(p^1,p^2)\), while the momenta \({\tilde{P}}\), \({\tilde{p}}_{1}\) and \({\tilde{p}}_{2}\) are defined as \({\tilde{p}}=(p^+,p_{\perp })\). Then the minus component of the momenta can be determined from their on-shell condition as \(p^{-}=(m^2+p_{\perp }^2)/p^{+}\).
It is necessary to stress that in this paper, we will only consider the leading order contributions. Introducing higher order corrections between the spectators and the quarks attached to electroweak current will spoil the diquark picture. In that case, decomposing the whole system into a scalar/axial-vector diquark as shown in Eq. (1) is not meaningful. Instead one should consider the dynamics of all three quarks, and some attempts can be found in Ref. [25].
\(\Psi ^{SS_{z}}\) is the momentum-space wave function and can be shown with the following equation,
here \(\Gamma \) is the coupling vertex of the decay quark \(Q_{1}\) and the diquark in the baryon state, and when the diquark is a scalar diquark, the coupling vertex is defined as \(\Gamma _{S}=1\). In Ref. [55], when an axial-vector diquark is involved, the vertex should be

In this work, \({{\bar{P}}}\) is the sum of the on-mass-shell momenta of the heavy quark Q and diquark, \({\bar{P}}=p_1+p_2\) and \({\bar{P}}^2=M_{0}^2\). Since the baryon, heavy quark and diquark cannot be on their mass shells simultaneously, the invariant mass \(M_0\) is different from the baryon mass M. The momentum of the baryon P and mass M satisfy the physical mass-shell condition \(M^2=P^2\) and \(\mathbf{{P}}^{2}+M^2= E^2\), while for the momentum \(\bar{P}\), we have \({\varvec{{\bar{\mathbf{P}}}}}^{2}+M^2\ne E^2\). \( m_1\) and \(m_2\) are the masses of the heavy quark and the diquark, respectively. In Eq. (2), \(\phi \) is a Gaussian-type function:
where \(e_1\) and \(e_2\) denote the energy of the heavy quark Q and diquark, in \({\bar{P}}\) rest frame. \(x_1\) and \(x_2\) are the light-front momentum fractions satisfying \(0<x_2<1\) and \(x_1+x_2=1\). In order to describe the internal motion of the constituent quarks, we introduce the internal momenta with
\(\vec k\) in the Eq. (4) is the internal momentum vector of diquark, and \(\vec k=(k_{2\bot },k_{2z})=(k_{\bot }, k_{z})\). The parameter \(\beta \) in Eq. (4) desicribes the momentum distributions among the constituent quarks which is listed in Table 4. Then the invariant mass square \(M_0^2\) can be expressed as a function of the internal variables \((x_{i},k_{i\bot })\),
With the help of \(M_0=e_1+e_2\), it is easy to obtain the expressions of \(e_i\) and \(k_z\) in terms of the internal variables \((x_{i},k_{i\bot })\) as,
In this work, we set \(x=x_2\) and thus \(x_1=1-x\).
In analogy to the \(1/2^{+}\) baryon case, a \(3/2^{+}\) baryon state has a similar expression to Eq. (1) except a different coupling vertex [56]:
where
With the help of Eqs. (1) and (2), the spin-1/2 to spin-1/2 transition matrix element with \(\mathrm {(V-A)}\) and tensor current can be derived as


With the help of Eqs. (1), (2) and (5), the spin-1/2 to spin-3/2 transition matrix element with \(\mathrm {(V-A)}\) and tensor current can be derived as


here \(p_{1}\) and \(p_{1}^{\prime }\) are the four-momentum of the initial and final quark, and \(p_2\) is the momentum of diquark, as shown in Fig. 3. P and \(P^{\prime }\) are the four-momentum of the initial baryons \({{\mathcal {B}}}\) and final baryon states \({{\mathcal {B}}}^{\prime }\), respectively. M and \(M^{\prime }\)are the masses of the initial and final baryon states, respectively. It is noted that, \(M_0\) and \(M_0^{\prime }\) are the invariant masses of the initial and final baryon states which are different from M and \(M^{\prime }\). \(q_{1}=u,d,s,c\) means the lighter quark in the final states shown in Fig. 3. When the diquark is a scalar diquark, the coupling vertex is defined as,
and when an axial-vector diquark is involved, the vertex should be

and
The \(1/2\rightarrow 1/2\) transition matrix elements can be parameterized as


Then the extraction of these form factors \(f_{1,2,3,S(A)}\) can be performed as Ref. [54]. Multiply \({\bar{u}}({\bar{P}},S_{z})({{\bar{\Gamma }}}^{\mu })_{i}u({\bar{P}}^{\prime },S_{z}^{\prime })\) and \({\bar{u}}(P,S_{z})(\Gamma ^{\mu })_{i}u(P^{\prime },S_{z}^{\prime })\) on the \(\langle {{\mathcal {B}}}^{\prime }_{f}(P^{\prime },S^{\prime }=\frac{1}{2},S_{z}^{\prime }) |{\bar{q}}_{1}\gamma _{\mu }Q_{1}|{{\mathcal {B}}}_{i}(P,S=\frac{1}{2},S_{z})\rangle \) part of Eq. (7) and Eq. (15), respectively. At the same time, the approximation \(P^{(\prime )}\rightarrow {\bar{P}}^{(\prime )}\) need to be taken for the integral. After summing the polarizations of the initial and final baryon states up, we can get the three linear equations as follows,

with \(({{\bar{\Gamma }}}^{\mu })_{i}=\{\gamma ^{\mu },{\bar{P}}^{\mu },{\bar{P}}^{\prime \mu }\}\) and \((\Gamma ^{\mu })_{i}=\{\gamma ^{\mu },P^{\mu },P^{\prime \mu }\}\). Using the above Eq. (17), we can get the specific expression of the form factors \(f_{1,2,3,S(A)}\) as follows:
with

The form factors \(g_{1,2,3,S(A)}\) can be calculated by the similar procedure,
with

Then tensor form factors \(f_{1,2,S(A)}^{T}\) and \(g_{1,2,S(A)}^{T}\) defined by Eq. (16) can also be extracted in the similar way with the form factors \(f_{1,2,3,S(A)}\) and \(g_{1,2,3,S(A)}\), the differences are only \((\Gamma ^{\mu })_{i}=\{\gamma ^{\mu },P^{\mu }\}\) and \(({{\bar{\Gamma }}}^{\mu })_{i}=\{\gamma ^{\mu },{\bar{P}}^{\mu }\}\),
with

The \(1/2\rightarrow 3/2\) transition matrix elements can be parameterized in a similar form as follows.


Here \(q^{\mu }=P^{\mu }-P^{\prime \mu }\) and \({{\mathcal {P}}}^{\mu }=P^{\mu }+P^{\prime \mu }\). In the previous work [13], the \(1/2\rightarrow 3/2\) transition matrix elements have been parameterized with form factors \(\mathtt {f}_{1,2,3,4}^{\prime (T)}\) and \(\mathtt {g}_{1,2,3,4}^{\prime (T)}\) in following form,
Then the form factors \(\mathtt {f}_{1,2,3,4}^{(T)}\) and \(\mathtt {g}_{1,2,3,4}^{(T)}\) defined by Eqs. (22)–(23) can be related with \(\mathtt {f}_{1,2,3,4}^{\prime (T)}\) and \(\mathtt {g}_{1,2,3,4}^{\prime (T)}\) defined by Eqs. (24) and (25) by the following formulas:
Multiplying Eq. (23) by \(q^{\mu }\) will yield
and one obtains \(\mathtt {f}_{3}^{T}(q^2)=\mathtt {g}_{3}^{T}(q^2)=0\). Then using Eqs. (26)–(29), one could get
These form factors \(\mathtt {f}_{1,2,3,4}^{\prime }\) and \(\mathtt {g}_{1,2,3,4}^{\prime }\) can be extracted in the following way [54]. Multiply \({\bar{u}}(P,S_{z})({{\bar{\Gamma }}}_{5}^{\mu \beta })_{i}u_{\beta }(P^{\prime },S_{z}^{\prime })\) and \({\bar{u}}(P,S_{z})(\Gamma _{5}^{\mu \beta })_{i}u_{\beta }(P^{\prime },S_{z}^{\prime })\) on the “\(\langle \mathcal{B}^{\prime *}_{f}(P^{\prime },S^{\prime }=\frac{3}{2},S_{z}^{\prime })|{\bar{q}}_{1}\gamma ^{\mu }Q_{1}|\mathcal{B}_{i}(P,S=\frac{1}{2},S_{z})\rangle \)” part of Eqs. (9) and (24), respectively. At the same time, the approximation \(P^{(\prime )}\rightarrow {\bar{P}}^{(\prime )}\) need to be taken for the integral. After summing the polarizations of the initial and final baryon states up, we can get the four equations as follows,

with \((\Gamma _{5}^{\mu \beta })_{i}=\{\gamma ^{\mu } P^{\beta },P^{\prime \mu }P^{\beta },P^{\mu }P^{\beta }, g^{\mu \beta }\}\gamma _{5}\) and \(({{\bar{\Gamma }}}_{5}^{\mu \beta })_{i}=\{\gamma ^{\mu }{\bar{P}} ^{\beta },{\bar{P}}^{\prime \mu }{\bar{P}}^{\beta },{\bar{P}}^{\mu }{\bar{P}} ^{\beta },g^{\mu \beta }\}\gamma _{5}\).
As shown in Refs. [56, 57], the spin sum of the vectorial spinors can be given as,

with
The analytic expression of form factors \(\mathtt {f}_{1,2,3,4}^{\prime }\) can be got by solving the above four equations in Eq. (33),
where \(H_i\) is defined as follows,

With the same method, one can obtain the form factors \(\mathtt {g}_{1,2,3,4}^{\prime }\). \(\mathtt {g}_{1}^{\prime }\) and \(\mathtt {g}_{3}^{\prime }\) are similar to \(\mathtt {f}_{1}^{\prime }\) and \(\mathtt {f}_{3}^{\prime }\) respectively except for \(M^{\prime }\rightarrow -M^{\prime }\) and \(H_{i}\rightarrow K_{i}\), and \(\mathtt {g}_{2}^{\prime }\) and \(\mathtt {g}_{4}^{\prime }\) are similar to \(\mathtt {f}_{2}^{\prime }\) and \(\mathtt {f}_{4}^{\prime }\) respectively except for \(M^{\prime }\rightarrow -M^{\prime }\) and \(H_{i}\rightarrow -K_{i}\). For example, we have
where \(K_i\) is defined by the following Eq. (40),

with \(({{\bar{\Gamma }}}^{\mu \beta })_{i}=\{\gamma ^{\mu }{\bar{P}}^{\beta },{\bar{P}}^{\prime \mu }{\bar{P}}^{\beta },{\bar{P}}^{\mu }{\bar{P}}^{\beta },g^{\mu \beta }\}\). Note that \(\mathtt {f}_{1,2,3,4}^{\prime T}\) and \(\mathtt {g}_{1,2,3,4}^{\prime T}\) should not be independent. Multiplying the Eq. (25) by \(q^{\mu }\) leads to
and the following two relations can be arrived,
With the above relations, \(\langle \mathcal{B}^{\prime }(P^{\prime },S_{z}^{\prime })|{\bar{q}}_{1}i\sigma _{\mu \nu }\frac{q^{\nu }}{M}(1+\gamma _{5})Q_{1}|\mathcal{B}(P,S_{z})\rangle \) can be parameterized with the form factors \(\mathtt {f}_{2,3,4}^{\prime T}\) and \(\mathtt {g}_{2,3,4}^{\prime T}\). These form factors \(\mathtt {f}_{2,3,4}^{\prime T}\) and \(\mathtt {g}_{2,3,4}^{\prime T}\) can be extracted in the same way as we have conducted on the form factors \(\mathtt {f}_{1,2,3,4}^{\prime }\) and \(\mathtt {g}_{1,2,3,4}^{\prime }\) [54]. Multiply \({\bar{u}}(P,S_{z})({{\bar{\Gamma }}}_{5}^{\mu \beta })_{i}u_{\beta }(P^{\prime },S_{z}^{\prime })\) and \({\bar{u}}(P,S_{z})(\Gamma _{5}^{\mu \beta })_{i}u_{\beta }(P^{\prime },S_{z}^{\prime })\) on the “\(\langle \mathcal{B}^{\prime }_{f}(P^{\prime },S^{\prime }=\frac{1}{2},S_{z}^{\prime }) |{\bar{q}}_{1}i\sigma _{\mu \nu }\frac{q^{\nu }}{M}Q_{1}|\mathcal{B}_{i}(P,S=\frac{1}{2},S_{z})\rangle \)” part of Eqs. (10) and (25), respectively. At the same time, the approximation \(P^{(\prime )}\rightarrow {\bar{P}}^{(\prime )}\) need to be taken for the integral. After summing the polarizations of the initial and final baryon states up, we can get the three equations as follows,

with \(({{\bar{\Gamma }}}_{5}^{\mu \beta })_{i}=\{\gamma ^{\mu }{\bar{P}}^{\beta },{\bar{P}}^{\prime \mu }{\bar{P}}^{\beta },g^{\mu \beta }\}\gamma _{5}\) and \((\Gamma _{5}^{\mu \beta })_{i}=\{\gamma ^{\mu }P^{\beta },P^{\prime \mu }P^{\beta },g^{\mu \beta }\}\gamma _{5}\).
Then the expressions of form factors \(\mathtt {f}_{2,3,4}^{\prime T}\) could be gained by solving the above three equations and are shown with the following formulas:
where \(H_i^{T}\) is defined in Eq. (48),

With the same method, one can obtain the form factors \(g_{2,3,4}^{\prime T}\). \(\mathtt {g}_{2}^{\prime T}\) and \(\mathtt {g}_{4}^{\prime T}\) are similar to \(\mathtt {f}_{2}^{\prime T}\) and \(\mathtt {f}_{4}^{\prime T}\) respectively except for \(M^{\prime }\rightarrow -M^{\prime }\) and \(H_{i}^{T}\rightarrow -K_{i}^{T}\). \(\mathtt {g}_{3}^{\prime T}\) is similar to \(\mathtt {f}_{3}^{\prime T}\) except for \(M^{\prime }\rightarrow -M^{\prime }\) and \(H_{i}^{T}\rightarrow K_{i}^{T}\). For example, we have
where \(K_i^{T}\) is defined by the following Eq. (50),

with \(({{\bar{\Gamma }}}^{\mu \beta })_{i}=\{\gamma ^{\mu }{\bar{P}}^{\beta },{\bar{P}}^{\prime \mu }{\bar{P}}^{\beta },g^{\mu \beta }\}\).
2.2 Flavor-spin wave functions
In the above section, we have presented the explicit expressions of form factors. However, a physical form factor should be a linear combination of the transition form factors with a scalar and an axial-vector diquark spectator.
and here \(c_{S}\) and \(c_{A}\) are the overlapping factors which are derived from the flavor spin wave functions of the initial and final baryon states with S and A corresponding to the scalar and the axial vector diquark spectator of these doubly heavy baryons decays. The hadronic matrix elements can be written as
and the form factors \(f_{i,S}\) and \(f_{i,A}\) extracted from Eq. (17) are involved with the transition matrix elements \(\langle q_{1}[Q_{2}q]_{S}|\Gamma _{\mu }|Q_{1}[Q_{2}q]_{S}\rangle \) and \(\langle q_{1}\{Q_{2}q\}_{A}|\Gamma _{\mu }|Q_{1}\{Q_{2}q\}_{A}\rangle \), respectively. Here the current \(\Gamma _{\mu }\) is \(\Gamma _{\mu }={{\bar{q}}}_1\gamma _{\mu }(1-\gamma _5)Q_1\) or \({{\bar{q}}}_1\sigma _{\mu \nu }\frac{q^{\nu }}{M}(1+\gamma _5)Q_1\). Eqs. (51) and (52) are for the \(1/2\rightarrow 1/2\) transitions. It is necessary to warn again that the above expression is based on the leading order results. Including the interactions among the weak current and the spectator diquark will spoil the decomposition into a scalar/axial-vector diquark.
For the transition \(1/2\rightarrow 3/2\), the diquark in the final state baryons can not be a scalar state, so the transition matrix element \(\langle q_{1}[Q_{2}q]_{S}|\Gamma _{\mu }|Q_{1}[Q_{2}q]_{S}\rangle \) is zero and the physical form factor is given as
In this section, via performing the inner product of the flavor-spin wave functions of the initial and final states, the overlapping factors \(c_{S}\) and \(c_{A}\) in Eqs. (51) and (53) can be calculated easily. For shortage of the paper, the detail calculation of the wave functions for the initial and final baryons is arranged in the Appendix A. The flavor spin wave functions for the doubly charmed SU(3) triplets \(\Xi _{cc}^{++}\), \(\Xi _{cc}^{+}\) and \(\Omega _{cc}^{+}\) are
here the two charm quarks noted by \(c^{1}\) and \(c^{2}\) are symmetric. The flavor spin wave functions of the doubly bottomed SU(3) triplets \(\Xi _{bb}^{0}\), \(\Xi _{bb}^{-}\) and \(\Omega _{bb}^{-}\) can be obtained through the replacement \(c\rightarrow b\). While the bottom-charm baryons could form two sets of SU(3) triplets, (\(\Xi _{bc},\Omega _{bc}\)) and (\(\Xi _{bc}^{\prime },\Omega _{bc}^{\prime }\)). The flavor spin wave functions of bottom-charm baryons (\(\Xi _{bc},\Omega _{bc}\)) can be given as
while the flavor spin wave functions of bottom-charm baryons (\(\Xi _{bc}^{\prime },\Omega _{bc}^{\prime }\)) are given as
The flavor-spin wave functions of the anti-triplet singly charmed baryons can be shown as follows,
while the flavor spin wave functions of the sextet of singly charmed baryons are demonstrated as
Then we can get the wave functions of the singly bottom baryons by changing c in Eqs. (57)–(58) to b. While for the baryons \({{\mathcal {B}}}^{*}\) with spin-3/2 in the final states, their flavor spin wave function are given as follows,
with \(q^{(\prime )}=u,d,s\), and \(Q^{(\prime )}=c,b\).
With the above wave functions of doubly heavy baryons and singly heavy baryons, the overlapping factors \(c_{S,A}\) for each transition can be got. The corresponding results of the overlapping factors \(c_{S,A}\) for the \(1/2\rightarrow 1/2\) transitions induced by the charged current and the FCNC in Eq. (52) are collected in Table 2. For the \(1/2\rightarrow 3/2\) transitions induced by the charged current and the FCNC, the numerical results of the overlapping factors \(c_{A}\) are listed in Table 3. Under SU(3) symmetry the doubly heavy baryons can be formed into triplets and the singly heavy baryons can be formed into an anti-triplet and a sextet. The overlapping factors \(c_{S,A}\) can be calculated with SU(3) approach, and the detail calculation can be found in the Appendix C. Using the SU(3) approach, one gets the same numerical results of \(c_{S(A)}\) as those listed in Tables 2 and 3. Then for a spin 1/2 finial state with a scalar and an axial-vector diquark, the physical form factors are then obtained by
where these form factors \(f_{i,S(A)}\), \(g_{i,S(A)}\), \(f_{i,S(A)}^{T}\) or \(g_{i,S(A)}^{T}\) are defined by Eqs. (15) and (16). However, for a spin 3/2 finial state with only an axial-vector diquark, the physical form factors are then obtained by
where these form factors \(\mathtt {f}_{i}\), \(\mathtt {g}_{i}\), \({\mathtt {f}}_{i}^{T}\) or \(\mathtt {g}_{i}^{T}\) are defined in Eqs. (22)–(23).
3 Numerical results of form factors
The masses of quarks are taken from Refs. [39,40,41,42,43,44,45,46,47],
The masses of diquark are approximatively taken as,
The masses of all baryons, lifetime of parent baryons and shape parameters \(\beta \) in Eq. (4) are collected in Table 4 [1, 4, 58,59,60,61,62,63].
\(q^2\) dependence of the form factors for the transition \(\Xi _{bb}^{0}\rightarrow \Sigma _{b}^{+}\). The first two graphs correspond to form factors with scalar diquarks, and the second two graphs correspond to form factors with axial-vector diquarks. The numerical result of F(0), \(\delta \) and \(m_{fit}\) are shown in Table 6
Using these analytical expression of form factors shown in Sect. 2.1 and the input parameters listed in Eqs. (63)–(64) and Table 4, one can calculate the form factors with the scalar or axial vector diquarks in Eqs. (12), (3) and (13). While for each form factors are functions of \(q^2\), in order to obtain the dependence of form factors on the momentum \(q^2\), we take the following parametrization scheme for \(b\rightarrow u,d,s,c\) processes,
here F(0) is the numerical result of form factor at \(q^2=0\), \(m_{\mathrm{fit}}\) and \(\delta \) are two parameters waiting for fitting from numerical result of form factor at different \(q^2\) values. When the fitting result of \(m_{\mathrm{fit}}\) is an imaginary result using the above parametrization scheme, we need to take the modified parametrization scheme as follows,
In the tables, we mark the imaginary results with superscripts “\(*\)”. Here \(F(q^2)\) in Eqs. (65) and (66), denotes the form factors \(f_{i,S(A)}^{(T)}\), \(g_{i,S(A)}^{(T)}\) defined by Eqs. (15)–(16) and \({\mathtt {f}}_{i}^{(T)}\), \(\mathtt {g}_{i}^{(T)}\) defined in Eqs. (22)–(23). In LFQM these form factors can be calculated in the un-physical region \(q^2=-q_{\perp }^2\le 0\) (the space-like region), in this work, we fit out the parameters \(m_{\mathrm{fit}}\) and \(\delta \), using the numerical results of form factors at \(q^2=\{-0.0001,-2,-4,-6,-8,-10\}\). As discussed in Refs. [25, 30, 31, 34, 35, 54, 55, 64,65,66], we shall extend them into physical region \(q^2\ge 0\) (the time-like region) analytically, using Eqs. (65) and (66). While for c quark decay processes, the single pole structure is assumed
for \(c\rightarrow u,~d,~s\) decays, \(m_{\mathrm{pole}}\)s are respectively 1.87, 1.87, 1.97 GeV.
For the transition induced by charged current \({1}/{2}\rightarrow {1}/{2}\), the results for form factors with a scalar diquark or an axial-vector diquark spectator are shown in Tables 5, 6 and 7. As shown in Eq. (15), the numerical results of the form factors can be used to calculate the physical hadronic transition matrix elements. We take \(\Xi _{bb}^{0}\rightarrow \Sigma _{b}^{+}\) as an example to show the \(q^2\)-dependence of form factors in Fig. 4. There is no singular point for the form factors \(f_{1,2,3}\) and \(g_{1,2,3}\) in the integration interval shown in Fig. 4.
For the FCNC transition \({1}/{2}\rightarrow {1}/{2}\), the results for form factors with a scalar diquark or an axial-vector diquark spectator are shown in Tables 8, 9 and 10. With the help of the results of the form factors and Eqs. (15)–(16), one can calculate the physical hadronic transition matrix elements. \(\Xi _{bb}^{0}\rightarrow \Lambda _{b}^{0}\) is taken as an example to show the \(q^2\)-dependence of these form factors which are depicted in Fig. 5. As one can see, these form factors are stable and no divergence exists in the integration interval.
For the charged current transition \({1}/{2}\rightarrow {3}/{2}\), the results for form factors with an axial-vector diquark spectator are shown in Tables 11 and 14. As shown in Eq. (22), the numerical results of the form factors can be used to calculate the physical hadronic transition matrix elements. In Fig. 6 we use \(\Xi _{bb}^{0}\rightarrow \Sigma _{b}^{*0}\) as an example to show the \(q^2\)-dependence of form factors. As shown in Fig. 6 these form factors are stable, which indicates our fitting result in the Tables 11 and 14 are reliable (Table 12).
For the FCNC transition \({1}/{2}\rightarrow {3}/{2}\), the results for form factors with an axial-vector diquark are shown in Tables 13, 16 and 15. As shown in Eqs. (22) and (23), the numerical results of the form factors can be used to calculate the physical hadronic transition matrix elements. To describe the dependence of form factors on \(q^2\), we take the transition \(\Omega _{bb}\rightarrow \Xi _{b}^{\prime *-}\) as an example shown in Fig. 7. The curves are all approaching to zero at large \(q^2\) stably (Tables 14, 15).
4 Semi-leptonic weak decays
For the charged current processes \(c\rightarrow d,s~l^{+}\nu _{l}\), the effective Hamiltonian is
and for \(b\rightarrow u,c~l^{-}{{\bar{\nu }}}_{l}\), the effective Hamiltonian has been given as
While for the FCNC processes \(b\rightarrow sl^{+}l^{-}\), the effective Hamiltonian can be given as
In Eqs. (68), (69) and (70), the Fermi constant \(G_F\) and the CKM matrix elements are taken from Ref. [67]:
The reader interested in the explicit forms of operators \(O_{i}\) in Eq. (70) can consult Ref. [68]. Wilson coefficients \(C_{i}\) for each operators \(O_{i}\) are calculated in the leading logarithmic approximation, with \(m_{W}=80.4\) GeV and \(\mu =m_{b,\mathrm{pole}}\) [68] and can be given as follows,
For the FCNC processes \({{\mathcal {B}}}_{b}\rightarrow {{\mathcal {B}}}_{s}^{\prime }l^{+}l^{-}\), the amplitude can be obtained in following form,
In Refs. [69,70,71], the signs before \(C_{7}^{\mathrm{eff}}\) are different. In this paper, we take the same sign with the ones in Refs. [69, 70], which is different from the one in Ref. [71]. In the above Eq. (73), \(C_{7}^{\mathrm{eff}}\) and \(C_{9}^{\mathrm{eff}}\) are obtained as [72]
where \({\hat{s}}=q^{2}/m_{b}^{2}\), \(C_{0}=C_{1}+3C_{2}+3C_{3}+C_{4}+3C_{5}+C_{6}\), and \({\hat{m}}_{c}=m_{c}/m_{b}\). The auxiliary functions h have been given as
While for the FCNC processes \(b\rightarrow d l^+l^-\), the corresponding effective Hamiltonian and amplitude can be achieved by taking a replacement \(s\rightarrow d\) similarly.
4.1 Decay widths
4.1.1 the charged current transition
For the transition induced by charged current, the kinematics are shown in Fig. 8, and the helicity amplitudes are defined by
here \(\epsilon _{\mu }\) and \(q_{\mu }\) are the polarization vector and four-momentum of the virtual propagator W, and \(\lambda _{W}\) means the polarization of the virtual propagator W. \(\lambda \) and \(\lambda ^{\prime }\) are the helicities of the baryon in the initial and final baryon states, respectively. The detail derivation process of helicity amplitudes can be found in Appendix B. These helicity amplitudes are related to the form factors by the following expressions.
The transition \(B_{i}(\lambda )\rightarrow B_{f}(\lambda ^{\prime })\) matrix elements are parameterized as shown in Eq. (15), and the helicity amplitudes of \(1/2\rightarrow 1/2\) charged current transition can be expressed with following equations,
$$\begin{aligned} HV_{\frac{1}{2},0}^{-\frac{1}{2}}&=-i\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}}\left( (M+M^{\prime })f_{1}^{\frac{1}{2}\rightarrow \frac{1}{2}}-\frac{q^{2}}{M}f_{2}^{\frac{1}{2}\rightarrow \frac{1}{2}}\right) ,\nonumber \\ HV_{\frac{1}{2},1}^{\frac{1}{2}}&=i\sqrt{2Q_{-}} \left( -f_{1}^{\frac{1}{2}\rightarrow \frac{1}{2}}+\frac{M+M^{\prime }}{M}f_{2}^ {\frac{1}{2}\rightarrow \frac{1}{2}}\right) ,\nonumber \\ HA_{\frac{1}{2},0}^{-\frac{1}{2}}&=-i\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}} \left( (M-M^{\prime })g_{1}^{\frac{1}{2}\rightarrow \frac{1}{2}} +\frac{q^{2}}{M}g_{2}^{\frac{1}{2}\rightarrow \frac{1}{2}}\right) ,\nonumber \\ HA_{\frac{1}{2},1}^{\frac{1}{2}}&=i\sqrt{2Q_{+}} \left( -g_{1}^{\frac{1}{2}\rightarrow \frac{1}{2}}-\frac{M-M^{\prime }}{M}g_{2}^{\frac{1}{2}\rightarrow \frac{1}{2}}\right) , \end{aligned}$$(77)with \(Q_{\pm }=2(P\cdot P^{\prime }\pm MM^{\prime })=(M\pm M^{\prime })^{2}-q^{2}\). Here \(f_i^{\frac{1}{2}\rightarrow \frac{1}{2}}\) and \(g_{i}^{\frac{1}{2}\rightarrow \frac{1}{2}}\) are the physical form factors which are defined by Eq. (61). M and \(M^{\prime }\) are the masses for the initial and final baryon. While the negative helicity amplitudes have the following relations with the corresponding positive ones,
$$\begin{aligned}&HV_{-\lambda ^{\prime },-\lambda _{W}}^{-\lambda }=HV_{\lambda ^{\prime },\lambda _{W}}^{\lambda }\quad \text {and}\nonumber \\&HA_{-\lambda ^{\prime },-\lambda _{W}}^{-\lambda }=-HA_{\lambda ^{\prime },\lambda _{W}}^{\lambda }. \end{aligned}$$(78)Then the total helicity amplitudes for (V-A) current can be shown as follows,
$$\begin{aligned} H_{\lambda ^{\prime },\lambda _{W}}^{\lambda }=HV_{\lambda ^{\prime },\lambda _{W}}^{\lambda }-HA_{\lambda ^{\prime },\lambda _{W}}^{\lambda }. \end{aligned}$$(79)The polarized differential decay widths can be given as
$$\begin{aligned} \frac{d\Gamma _{L}}{dq^{2}}&=\frac{G_{F}^{2}|V_{CKM}|^{2}}{(2\pi )^{3}}\frac{q^{2}|\vec {P}^{\prime }|}{24M^{2}} \Bigg (\Bigg |H_{\frac{1}{2},0}^{-\frac{1}{2}}\Bigg |^{2}{+}\Bigg |H_{-\frac{1}{2},0}^{\frac{1}{2}}\Bigg |^{2}\Bigg ), \end{aligned}$$(80)$$\begin{aligned} \frac{d\Gamma _{T}}{dq^{2}}&=\frac{G_{F}^{2}|V_{CKM}|^{2}}{(2\pi )^{3}}\frac{q^{2}|\vec {P}^{\prime }|}{24M^{2}} \Bigg (\Bigg |H_{\frac{1}{2},1}^{\frac{1}{2}}\Bigg |^{2}+\Bigg |H_{-\frac{1}{2},-1}^{-\frac{1}{2}}\Bigg |^{2}\Bigg ), \end{aligned}$$(81)with \(|\vec {P}^{\prime }|=\sqrt{Q_{+}Q_{-}}/2M\).
The \(B_{i}(\lambda )\rightarrow B_{f}^{*}(\lambda ^{\prime })\) transition matrix element are parameterized with Eq. (22), and the helicity amplitudes of the transitions \({1}/{2}\rightarrow {3}/{2}\) induced by charged current can be expressed with following equations,
$$\begin{aligned} HV_{3/2,1}^{-1/2}= & {} - i\sqrt{Q_{-}}f_{4}^{\frac{1}{2}\rightarrow \frac{3}{2}},\nonumber \\ HV_{1/2,1}^{1/2}= & {} i\sqrt{\frac{Q_{-}}{3}}\left[ f_{4}^{\frac{1}{2} \rightarrow \frac{3}{2}}-\frac{Q_{+}}{MM^{\prime }}f_{1}^{\frac{1}{2}\rightarrow \frac{3}{2}}\right] , \end{aligned}$$(82)$$\begin{aligned} HV_{1/2,0}^{-1/2}= & {} i\sqrt{\frac{2}{3}}\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}} \Bigg [\frac{M^2-M^{\prime 2}-q^2}{2M^{\prime }}f_{4}^{\frac{1}{2} \rightarrow \frac{3}{2}}\nonumber \\&\quad -\frac{M- M^{\prime }}{2MM^{\prime }}Q_{+}f_{1}^{\frac{1}{2}\rightarrow \frac{3}{2}}\nonumber \\&\quad -\frac{Q_{+}Q_{-}}{2M^{2}M^{\prime }}f_{2}^{\frac{1}{2}\rightarrow \frac{3}{2}}\Bigg ], \end{aligned}$$(83)$$\begin{aligned} HA_{3/2,1}^{-1/2}= & {} i\sqrt{Q_{+}}f_{4}^{\frac{1}{2}\rightarrow \frac{3}{2}},\nonumber \\ HA_{1/2,1}^{1/2}= & {} i\sqrt{\frac{Q_{+}}{3}}\left[ g_{4}^{\frac{1}{2}\rightarrow \frac{3}{2}} -\frac{Q_{-}}{MM^{\prime }}g_{1}^{\frac{1}{2}\rightarrow \frac{3}{2}}\right] , \end{aligned}$$(84)$$\begin{aligned} HA_{1/2,0}^{-1/2}= & {} - i\sqrt{\frac{2}{3}}\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}} \Bigg [\frac{M^2-M^{\prime 2}-q^2}{2M^{\prime }}g_{4}^{\frac{1}{2} \rightarrow \frac{3}{2}}\nonumber \\&\quad + \frac{M+ M^{\prime }}{2MM^{\prime }} Q_{-}g_{1}^{\frac{1}{2}\rightarrow \frac{3}{2}}\nonumber \\&\quad -\frac{Q_{+}Q_{-}}{2M^{2}M^{\prime }} g_{2}^{\frac{1}{2}\rightarrow \frac{3}{2}}\Bigg ], \end{aligned}$$(85)here \(f_i^{\frac{1}{2}\rightarrow \frac{3}{2}}\) and \(g_{i}^{\frac{1}{2}\rightarrow \frac{3}{2}}\) are physics form factors introduced with Eq. (62). M and \(M^{\prime }\) are the masses of the initial and final baryon states, respectively. While the negative helicity amplitudes have the following relations with the corresponding positive ones,
$$\begin{aligned} HV_{-\lambda ^{\prime },-\lambda _{W}}^{-\lambda }= & {} - HV_{\lambda ^{\prime },\lambda _{W}}^{\lambda }\quad \text {and} \quad \nonumber \\ HA_{-\lambda ^{\prime },-\lambda _{W}}^{-\lambda }= & {} HA_ {\lambda ^{\prime },\lambda _{W}}^{\lambda }. \end{aligned}$$(86)Then we can get the total helicity amplitudes,
$$\begin{aligned} H_{\lambda ^{\prime },\lambda _{W}}^{\lambda }= HV_{\lambda ^{\prime },\lambda _{W}}^{\lambda } -HA_{\lambda ^{\prime },\lambda _{W}}^{\lambda }. \end{aligned}$$(87)The polarized differential decay widths can be given as
$$\begin{aligned} \frac{d\Gamma _{L}}{dq^2}= & {} \frac{G_{F}^{2}}{(2\pi )^{3}}|V_{\mathrm{CKM}}|^{2}\frac{q^{2}|\vec {P}^{\prime }|}{24M^2}\Bigg [\Bigg |H_{1/2,0}^{-1/2}\Bigg |^{2}{+}\Bigg |H_{-1/2,0}^{1/2}\Bigg |^{2}\Bigg ],\nonumber \\ \end{aligned}$$(88)$$\begin{aligned} \frac{d\Gamma _{T}}{dq^2}= & {} \frac{G_{F}^{2}}{(2\pi )^{3}}|V_{\mathrm{CKM}}|^{2} \frac{q^{2}|\vec {P}^{\prime }|}{24M^2}\Bigg [\Bigg |H_{1/2,1}^{1/2}|^{2}+\Bigg |H_{-1/2,-1}^{-1/2}\Bigg |^{2}\nonumber \\&+\Bigg |H_{3/2,1}^{-1/2}\Bigg |^{2}+\Bigg |H_{-3/2,-1}^{1/2}\Bigg |^{2}\Bigg ]. \end{aligned}$$(89)
\(q^2\) dependence of the form factors for \(\Xi _{bb}^{0}\rightarrow \Lambda _{b}^{0}\) . The first four graphs correspond to form factors with scalar diquark, the last four graphs correspond to form factors with axial-vector diquark. Here the numerical results of F(0), \(\delta \) and \(m_{fit}\) are shown in Table 10
\(q^2\) dependence of the transition \(\Xi _{bb}\rightarrow \Sigma _{b}^{*}\) form factors. The numerical result of the parameters F(0), \(\delta \) and \(m_{fit}\) are shown in Table 14
\(q^2\) dependence of the transition \(\Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime *-}\) form factors. The numerical result of the parameters F(0), \(\delta \) and \(m_{fit}\) are shown in Table 16
4.1.2 The FCNC transition
For the transition induced by FCNC, we adopt the helicity amplitudes as follows,
and
here \(\epsilon _{\mu }\) and \(q_{\mu }\) are the polarization vector and four-momentum of the virtual vector propagator V, and \(\lambda _{V}\) means the polarization of the virtual vector propagator V. \(\lambda \) and \(\lambda ^{\prime }\) are the helicities of the baryon in the initial and final baryon states, respectively. In the following, the superscripts “\({{\mathcal {V}}}_{l}\)” and “\({{\mathcal {A}}}_{l}\)” denote the corresponding leptonic counterparts \({\bar{l}}\gamma ^{\mu }l\) and \({\bar{l}}\gamma ^{\mu }\gamma _{5}l\), respectively.
The transition \(B_{i}(\lambda )\rightarrow B_{f}(\lambda ^{\prime })\) matrix elements are parameterized with Eqs. (15)–(16), and the helicity amplitudes of \(1/2\rightarrow 1/2\) induced by FCNC transition can be obtained with following expressions,
$$\begin{aligned} HV_{\frac{1}{2},0}^{{{\mathcal {V}}}_{l},-\frac{1}{2}}&=-i\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}}\left( (M+M^{\prime })F_{1}^{{{\mathcal {V}}}_{l}} -\frac{q^{2}}{M}F_{2}^{{{\mathcal {V}}}_{l}}\right) ,\nonumber \\ HV_{\frac{1}{2},1}^{{{\mathcal {V}}}_{l},\frac{1}{2}}&=i\sqrt{2Q_{-}}\left( -F_{1}^{{{\mathcal {V}}}_{l}}+ \frac{M+M^{\prime }}{M}F_{2}^{{{\mathcal {V}}}_{l}}\right) ,\nonumber \\ HA_{\frac{1}{2},0}^{{{\mathcal {V}}}_{l},-\frac{1}{2}}&=-i\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}}\left( (M-M^{\prime })G_{1}^ {{{\mathcal {V}}}_{l}}+\frac{q^{2}}{M}G_{2}^{{{\mathcal {V}}}_{l}}\right) ,\nonumber \\ HA_{\frac{1}{2},1}^{{{\mathcal {V}}}_{l},\frac{1}{2}}&=i\sqrt{2Q_{+}}\left( -G_{1}^{{{\mathcal {V}}}_{l}}-\frac{M-M^{\prime }}{M}G_{2}^ {{{\mathcal {V}}}_{l}}\right) ,\nonumber \\ \end{aligned}$$(92)and
$$\begin{aligned} HV_{-\lambda ^{\prime },-\lambda _{V}}^{{{\mathcal {V}}}_{l},-\lambda }= & {} HV_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {V}}}_{l},\lambda }, \quad HA_{-\lambda ^{\prime },-\lambda _{V}}^{{{\mathcal {V}}}_{l},-\lambda } = -HA_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {V}}}_{l},\lambda }.\nonumber \\ \end{aligned}$$(93)where the “HV” and “HA” are corresponding to the \(\Gamma ^{\mu }\) and \(\Gamma ^{\mu }\gamma _{5}\) parts in Eq. (90), respectively. The total helicity amplitude can be given as
$$\begin{aligned} H_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {V}}}_{l},\lambda }=HV_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {V}}}_{l},\lambda }-HA_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {V}}}_{l},\lambda }. \end{aligned}$$(94)The specific expressions of \(H_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {A}}}_{l},\lambda }\) are similar with the ones of \(H_{\lambda ^{\prime },\lambda _{V}}^{V,\lambda }\), except
$$\begin{aligned} F_{i}^{{{\mathcal {V}}}_{l}} \rightarrow F_{i}^{{{\mathcal {A}}}_{l}} \quad \mathrm {and} \quad G_{i}^{{{\mathcal {V}}}_{l}} \rightarrow G_{i}^{{{\mathcal {A}}}_{l}}. \end{aligned}$$(95)Furthermore, the timelike polarizations of the virtual vector propagator V for the helicity amplitudes, \(H^{{{\mathcal {A}}}_{l}}_{t}\) are necessary for the transitions induced by FCNC,
$$\begin{aligned} HV_{-\frac{1}{2},t}^{{{\mathcal {A}}}_{l},\frac{1}{2}}&=HV_{\frac{1}{2},t}^ {{{\mathcal {A}}}_{l},-\frac{1}{2}}\nonumber \\&=-i\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}} \left( (M-M^{\prime })F_{1}^{{{\mathcal {A}}}_{l}} +\frac{q^{2}}{M}F_{3}^{{{\mathcal {A}}}_{l}}\right) ,\nonumber \\ -HA_{-\frac{1}{2},t}^{{{\mathcal {A}}}_{l},\frac{1}{2}}&= HA_{\frac{1}{2},t}^{{{\mathcal {A}}}_{l},-\frac{1}{2}}\nonumber \\&=-i\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}}\left( (M+M^{\prime }) G_{1}^{{{\mathcal {A}}}_{l}}-\frac{q^{2}}{M}G_{3}^{{{\mathcal {A}}}_{l}} \right) \end{aligned}$$(96)and
$$\begin{aligned} H_{\lambda ^{\prime },t}^{{{\mathcal {A}}}_{l},\lambda }=HV_{\lambda ^{\prime },t}^{{{\mathcal {A}}}_{l},\lambda }-HA_{\lambda ^{\prime },t}^{{{\mathcal {A}}}_{l},\lambda }. \end{aligned}$$(97)In the above Eq. (92–97), the following notations have been introduced:
$$\begin{aligned} F_{1}^{{{\mathcal {V}}}_{l}}(q^{2})\equiv & {} C_{9}^{\mathrm{eff}}(q^{2})f_{1}^{\frac{1}{2}\rightarrow \frac{1}{2}}(q^{2})\nonumber \\&-C_{7}^{\mathrm{eff}}\frac{2m_{b}}{M^{\prime }-M}f_{1}^{\frac{1}{2}\rightarrow \frac{1}{2},T}(q^{2}),\nonumber \\ F_{2}^{{{\mathcal {V}}}_{l}}(q^{2})\equiv & {} C_{9}^{\mathrm{eff}}(q^{2})f_{2}^{\frac{1}{2}\rightarrow \frac{1}{2}}(q^{2})\nonumber \\&-C_{7}^{\mathrm{eff}}\frac{2m_{b}M}{q^{2}}f_{2}^{\frac{1}{2}\rightarrow \frac{1}{2},T}(q^{2}),\nonumber \\ G_{1}^{{{\mathcal {V}}}_{l}}(q^{2})\equiv & {} C_{9}^{\mathrm{eff}}(q^{2})g_{1}^{\frac{1}{2}\rightarrow \frac{1}{2}}(q^{2})\nonumber \\&+C_{7}^{\mathrm{eff}}\frac{2m_{b}}{M^{\prime }+M}g_{1}^{\frac{1}{2}\rightarrow \frac{1}{2},T}(q^{2}),\nonumber \\ G_{2}^{{{\mathcal {V}}}_{l}}(q^{2})\equiv & {} C_{9}^{\mathrm{eff}}(q^{2})g_{2}^{\frac{1}{2}\rightarrow \frac{1}{2}}(q^{2})\nonumber \\&+C_{7}^{\mathrm{eff}}\frac{2m_{b}M}{q^{2}}g_{2}^{\frac{1}{2}\rightarrow \frac{1}{2},T}(q^{2}), \end{aligned}$$(98)and
$$\begin{aligned} F_{i}^{{{\mathcal {A}}}_{l}}(q^{2})\equiv & {} C_{10}f_{i}^{\frac{1}{2}\rightarrow \frac{1}{2}}(q^{2}),\nonumber \\ G_{i}^{{{\mathcal {A}}}_{l}}(q^{2})\equiv & {} C_{10}g_{i}^{\frac{1}{2}\rightarrow \frac{1}{2}}(q^{2})\quad (i=1,2,3). \end{aligned}$$(99)Here \(f_{i}^{\frac{1}{2}\rightarrow \frac{1}{2},(T)}(q^2)\) and \(g_{i}^{\frac{1}{2}\rightarrow \frac{1}{2},(T)}(q^2)\) are the physical form factors illuminated by Eq. (61). The longitudinally and transversely polarized differential decay widths read,
$$\begin{aligned} \frac{d\Gamma _{L}}{dq^{2}}= & {} \frac{G_{F}^{2}|V_\mathrm{CKM}|^2\alpha _{em}^{2}|\vec {P} ^{\prime }||\vec {p}_{1}|}{24(2\pi )^{5}M^{2}\sqrt{q^{2}}}\nonumber \\&\times \Bigg \{\left( q^{2}+2m_{l}^{2}\right) \Bigg (\Bigg |H_{-\frac{1}{2},0}^ {{{\mathcal {V}}}_{l},\frac{1}{2}}\Bigg |^{2}+|H_{\frac{1}{2},0} ^{{{\mathcal {V}}}_{l},-\frac{1}{2}}\Bigg |^{2}\Bigg )\nonumber \\&+\left( q^{2}-4m_{l}^{2}\right) \Bigg (\Bigg |H_{-\frac{1}{2},0}^{{{\mathcal {A}}}_{l}, \frac{1}{2}}\Bigg |^{2}+|H_{\frac{1}{2},0}^{{{\mathcal {A}}}_{l}, -\frac{1}{2}}\Bigg |^{2}\Bigg )\nonumber \\&+6m_{l}^{2}\Bigg (\Bigg |H_{-\frac{1}{2},t}^{{{\mathcal {A}}}_{l}, \frac{1}{2}}|^{2}+\Bigg |H_{\frac{1}{2},t}^{{{\mathcal {A}}}_{l}, -\frac{1}{2}}\Bigg |^{2}\Bigg )\Bigg \}, \end{aligned}$$(100)$$\begin{aligned} \frac{d\Gamma _{T}}{dq^{2}}= & {} \frac{G_{F}^{2}|V_{\mathrm{CKM}}|^2\alpha _{em}^{2}| \vec {P}^{\prime }||\vec {p}_{1}|}{24(2\pi )^{5}M^{2}\sqrt{q^{2}}}\nonumber \\&\Bigg \{(q^{2}+2m_{l}^{2})(|H_{\frac{1}{2},1} ^{{{\mathcal {V}}}_{l},\frac{1}{2}}|^{2}+|H_{-\frac{1}{2},-1}^ {{{\mathcal {V}}}_{l},-\frac{1}{2}}|^{2})\nonumber \\&+(q^{2}-4m_{l}^{2})(|H_{\frac{1}{2},1}^ {{{\mathcal {A}}}_{l},\frac{1}{2}}|^{2}+|H_ {-\frac{1}{2},-1}^{{{\mathcal {A}}}_{l},- \frac{1}{2}}|^{2})\Bigg \}. \end{aligned}$$(101)with \(V_{\mathrm{CKM}}=V_{tb}V_{ts}^{*}\) for \(b\rightarrow s\) processes, \(V_{\mathrm{CKM}}=V_{tb}V_{td}^{*}\) for \(b\rightarrow d\) processes and \(|\vec {p}_{1}|=\frac{1}{2}\sqrt{q^2-4m_{l}^2}\).
The transition \({1}/{2}\rightarrow {3}/{2}\) matrix elements are parameterized with Eqs. (22)–(23), and the helicity amplitudes induced by FCNC can be given by the following expressions,
$$\begin{aligned} HV_{3/2,1}^{{{\mathcal {V}}}_{l},-1/2}= & {} - i\sqrt{Q_{-}}{{\mathcal {F}}}_{4}^{{{\mathcal {V}}}_{l}},\nonumber \\ HV_{1/2,1}^{{{\mathcal {V}}}_{l},1/2}= & {} i\sqrt{\frac{Q_{-}}{3}}\left[ {{\mathcal {F}}}_ {4}^{{{\mathcal {V}}}_{l}}-\frac{Q_{+}}{MM^{\prime }}{{\mathcal {F}}}_{1} ^{{{\mathcal {V}}}_{l}}\right] , \end{aligned}$$(102)$$\begin{aligned} HV_{1/2,0}^{{{\mathcal {V}}}_{l},-1/2}= & {} i\sqrt{\frac{2}{3}}\frac{\sqrt{Q_{-}}}{\sqrt{q^{2}}} \Bigg [\frac{M^2-M^{\prime 2}-q^2}{2M^{\prime }} {{\mathcal {F}}}_{4}^{{{\mathcal {V}}}_{l}}\nonumber \\&-\frac{M- M^{\prime }}{2MM^{\prime }}Q_{+}{{\mathcal {F}}}_{1}^ {{{\mathcal {V}}}_{l}}\nonumber \\&-\frac{Q_{+}Q_{-}}{2M^{2}M^{\prime }} {{\mathcal {F}}}_{2}^{{{\mathcal {V}}}_{l}}\Bigg ], \end{aligned}$$(103)$$\begin{aligned} HA_{3/2,1}^{{{\mathcal {V}}}_{l},-1/2}= & {} i\sqrt{Q_{+}}{{\mathcal {G}}}_{4}^{{{\mathcal {V}}}_{l}},\quad HA_{1/2,1}^{{{\mathcal {V}}}_{l},1/2} \nonumber \\= & {} i\sqrt{\frac{Q_{+}}{3}}\left[ {{\mathcal {G}}}_{4} ^{{{\mathcal {V}}}_{l}}-\frac{Q_{-}}{MM^{\prime }}{ {\mathcal {G}}}_{1}^{{{\mathcal {V}}}_{l}}\right] , \end{aligned}$$(104)$$\begin{aligned} HA_{1/2,0}^{{{\mathcal {V}}}_{l},-1/2}= & {} - i\sqrt{\frac{2}{3}}\frac{\sqrt{Q_{+}}}{\sqrt{q^{2}}} \Bigg [\frac{M^2-M^{\prime 2}-q^2}{2M^{\prime }} {{\mathcal {G}}}_{4}^{{{\mathcal {V}}}_{l}}\nonumber \\&+\frac{M+ M^{\prime }}{2MM^{\prime }}Q_{-} {{\mathcal {G}}}_{1}^{{{\mathcal {V}}}_{l}}-\frac{Q_{+}Q_{-}}{2M^{2}M^{\prime }} {{\mathcal {G}}}_{2}^{{{\mathcal {V}}}_{l}}\Bigg ].\nonumber \\ \end{aligned}$$(105)and
$$\begin{aligned}&HV_{-\lambda ^{\prime },-\lambda _{W}}^{{{\mathcal {V}}}_{l},-\lambda }=- HV_{\lambda ^{\prime },\lambda _{W}}^{{{\mathcal {V}}}_{l},\lambda },\nonumber \\&HA_{-\lambda ^{\prime },-\lambda _{W}}^ {{{\mathcal {V}}}_{l},-\lambda }=HA_{\lambda ^{\prime }, \lambda _{W}}^{{{\mathcal {V}}}_{l},\lambda }. \end{aligned}$$(106)where the “HV” and “HA” are corresponding to the \(\Gamma ^{\mu }\) and \(\Gamma ^{\mu }\gamma _{5}\) parts in Eq. (90), respectively. Then we can get the total helicity amplitudes,
$$\begin{aligned} H_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {V}}}_{l},\lambda }=HV_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {V}}}_{l},\lambda }-HA_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {V}}}_{l},\lambda }. \end{aligned}$$(107)The specific expressions of \(H_{\lambda ^{\prime },\lambda _{V}}^{{{\mathcal {A}}}_{l},\lambda }\) are similar with the ones of \(H_{\lambda ^{\prime },\lambda _{V}}^{V,\lambda }\), except
$$\begin{aligned} {{\mathcal {F}}}_{i}^{{{\mathcal {V}}}_{l}} \rightarrow {{\mathcal {F}}}_{i}^{{{\mathcal {A}}}_{l}}\quad \mathrm {and}\quad {{\mathcal {G}}}_{i}^{{{\mathcal {V}}}_{l}} \rightarrow {{\mathcal {G}}}_{i}^{{{\mathcal {A}}}_{l}}. \end{aligned}$$(108)Furthermore, the time-like polarizations of the virtual vector propagator V for the helicity amplitudes, \(H^{{{\mathcal {A}}}_{l}}_{t}\) are necessary for the transitions induced by FCNC,
$$\begin{aligned} -HV_{-\frac{1}{2},t}^{{{\mathcal {A}}}_{l},\frac{1}{2}}&=HV_{\frac{1}{2},t}^{{{\mathcal {A}}}_{l},-\frac{1}{2}}\nonumber \\&=i\sqrt{\frac{2}{3}}\sqrt{Q_{+}}\frac{Q_{-}}{2MM^{\prime }}\frac{M^2-M^{\prime 2}}{M}{{\mathcal {F}}}_3^{{{\mathcal {A}}}_{l}},\nonumber \\ HA_{-\frac{1}{2},t}^{{{\mathcal {A}}}_{l},\frac{1}{2}}&= HA_{\frac{1}{2},t}^{{{\mathcal {A}}}_{l},-\frac{1}{2}}\nonumber \\&=-i\sqrt{\frac{2}{3}}\sqrt{Q_{-}}\frac{Q_{+}}{2MM^{\prime }}\frac{M^2-M^{\prime 2}}{M}{{\mathcal {G}}}_3^{{{\mathcal {A}}}_{l}} \end{aligned}$$(109)and
$$\begin{aligned} H_{\lambda ^{\prime },t}^{{{\mathcal {A}}}_{l},\lambda }=HV_{\lambda ^{\prime },t}^{{{\mathcal {A}}}_{l},\lambda }-HA_{\lambda ^{\prime },t}^{{{\mathcal {A}}}_{l},\lambda }. \end{aligned}$$(110)In Eqs. (102–110), the following notations are introduced.
$$\begin{aligned} {{\mathcal {F}}}_{i}^{{{\mathcal {V}}}_{l}}(q^{2})\equiv & {} C_{9}^{\mathrm{eff}}(q^{2})f_{i}^{\frac{1}{2}\rightarrow \frac{3}{2}}(q^{2})\nonumber \\&-C_{7}^{\mathrm{eff}}\frac{2m_{b}M}{q^{2}}f_{i}^{\frac{1}{2}\rightarrow \frac{3}{2},T}(q^{2}),\nonumber \\ {{\mathcal {G}}}_{i}^{{{\mathcal {V}}}_{l}}(q^{2})\equiv & {} C_{9}^{\mathrm{eff}}(q^{2})g_{i}^{\frac{1}{2}\rightarrow \frac{3}{2}}(q^{2})\nonumber \\&+C_{7}^{\mathrm{eff}}\frac{2m_{b}M}{q^{2}}g_{i}^{\frac{1}{2}\rightarrow \frac{3}{2},T}(q^{2}),\nonumber \\ {{\mathcal {F}}}_{i}^{{{\mathcal {A}}}_{l}}(q^{2})\equiv & {} C_{10}f_{i}^{\frac{1}{2}\rightarrow \frac{3}{2}}(q^{2}),\nonumber \\ {{\mathcal {G}}}_{i}^{{{\mathcal {A}}}_{l}}(q^{2})\equiv & {} C_{10}g_{i}^{\frac{1}{2}\rightarrow \frac{3}{2}}(q^{2}),\quad (i=1,2,3,4). \end{aligned}$$(111)Here \(f_{i}^{\frac{1}{2}\rightarrow \frac{3}{2},(T)}(q^2)\) and \(g_{i}^{\frac{1}{2}\rightarrow \frac{3}{2},(T)}(q^2)\) are physics form factors illuminated by Eq. (62). The longitudinally and transversely polarized differential decay widths read
$$\begin{aligned} \frac{d\Gamma _{L}}{dq^{2}}= & {} \frac{G_{F}^{2}|V_\mathrm{CKM}|^2\alpha _{em}^{2}|\vec {P}^{\prime }||\vec {p}_{1}|}{24(2\pi )^{5}M^{2}\sqrt{q^{2}}}\nonumber \\&\times \Bigg \{\left( q^{2}+2m_{l}^{2}\right) \Bigg (\Bigg |H_{-\frac{1}{2},0}^ {{{\mathcal {V}}}_{l},\frac{1}{2}}\Bigg |^{2}+\Bigg |H_{\frac{1}{2},0} ^{{{\mathcal {V}}}_{l},-\frac{1}{2}}\Bigg |^{2}\Bigg ) \nonumber \\&+\left( q^{2}-4m_{l}^{2}\right) \Bigg (\Bigg |H_{-\frac{1}{2},0}^{{{\mathcal {A}}}_{l}, \frac{1}{2}}\Bigg |^{2}+\Bigg |H_{\frac{1}{2},0}^{{{\mathcal {A}}}_{l}, -\frac{1}{2}}\Bigg |^{2}\Bigg )\nonumber \\&+6m_{l}^{2}\Bigg (\Bigg |H_{-\frac{1}{2},t}^{{{\mathcal {A}}}_{l}, \frac{1}{2}}\Bigg |^{2}+\Bigg |H_{\frac{1}{2},t}^{{{\mathcal {A}}}_{l}, -\frac{1}{2}}\Bigg |^{2}\Bigg )\Bigg \}, \end{aligned}$$(112)$$\begin{aligned} \frac{d\Gamma _{T}}{dq^{2}}= & {} \frac{G_{F}^{2}|V_{\mathrm{CKM}}|^2\alpha _{em}^{2}|\vec {P}^{\prime } ||\vec {p}_{1}|}{24(2\pi )^{5}M^{2}\sqrt{q^{2}}}\nonumber \\&\times \Bigg \{\left( q^{2}+2m_{l}^{2}\right) \Bigg (\Bigg |H_{\frac{1}{2},1}^{ {{\mathcal {V}}}_{l},\frac{1}{2}}\Bigg |^{2}+\Bigg |H_{-\frac{1}{2},-1}^{{{ \mathcal {V}}}_{l},-\frac{1}{2}}\Bigg |^{2}\nonumber \\&+\Bigg |H_{\frac{3}{2},1}^{{{\mathcal {V}}}_{l}, -\frac{1}{2}}\Bigg |^{2}+\Bigg |H_{-\frac{3}{2},-1}^{{{\mathcal {V}}}_{l}, \frac{1}{2}}\Bigg |^{2}\Bigg )\nonumber \\&+\left( q^{2}-4m_{l}^{2}\right) \Bigg (\Bigg |H_{\frac{1}{2},1}^{{{\mathcal {A}}}_{l}, \frac{1}{2}}\Bigg |^{2}+\Bigg |H_{-\frac{1}{2},-1}^{{{\mathcal {A}}}_{l},-\frac{1}{2}}\Bigg |^{2}\nonumber \\&+\Bigg |H_{\frac{3}{2},1}^{{{\mathcal {A}}}_{l},-\frac{1}{2}}\Bigg |^{2}+\Bigg |H_{-\frac{3}{2},-1}^{{{\mathcal {A}}}_{l},\frac{1}{2}} \Bigg |^{2}\Bigg )\Bigg \}. \end{aligned}$$(113)with \(V_{\mathrm{CKM}}=V_{tb}V_{ts}^{*}\) for \(b\rightarrow s\) processes, \(V_{\mathrm{CKM}}=V_{tb}V_{td}^{*}\) for \(b\rightarrow d\) processes and \(|\vec {p}_{1}|=\frac{1}{2}\sqrt{q^2-4m_{l}^2}\).
In the end, the total differential decay width can be written as
then we can calculate total width using the following integral,
where \(q^2_{\mathrm{min}}= 0\) for these decays with charged current, while \(q^2_{\mathrm{min}}=4m_{l}^2\) for other decays with FCNC. At the same time, the ratio of the longitudinal to transverse decay rates \(\Gamma _{L}/\Gamma _{T}\) can be calculated.
4.2 Results for semi-leptonic decays
For the transition \({1}/{2}\rightarrow {1}/{2}\) with \(\mathrm {V-A}\) current, the integrated partial decay widths, the relevant branching ratios and \(\Gamma _{L}/\Gamma _{T}\)s are shown in Table 16. The dependence of \(q^2\) of the differential decay widths can be shown in Fig. 9.
For the transition \({1}/{2}\rightarrow {1}/{2}\) induced by FCNC, the integrated partial decay widths, the relevant branching ratios and \(\Gamma _{L}/\Gamma _{T}\)s are shown in Table 17. The dependence of \(q^2\) of the differential decay widths can be shown in Fig. 10.
For the transition \({1}/{2}\rightarrow {3}/{2}\) with \(\mathrm {V-A}\) current, the integrated partial decay widths, the relevant branching ratios and \(\Gamma _{L}/\Gamma _{T}\)s are shown in Table 18. The dependence of \(q^2\) of the differential decay widths can be shown in Fig. 11.
For the transition \({1}/{2}\rightarrow {3}/{2}\) with FCNC, the integrated partial decay widths, the relevant branching ratios and \(\Gamma _{L}/\Gamma _{T}\)s are shown in Table 19. The dependence of \(q^2\) of the differential decay widths can be shown with Fig. 12.
Some comments on the results for phenomenological observables are given as follows.
It can be seen in Tables 16, 17, 18 and 19 that the decay widths for the four cases have the following hierarchical difference.
$$\begin{aligned}&\Gamma \mathrm{(the~transition~1/2\rightarrow 1/2~with~charged~current)}\\&\quad>\Gamma \mathrm{(the~transition~1/2\rightarrow 3/2~with~charged~current)}\\&\quad>\Gamma \mathrm{(the~transition~1/2\rightarrow 1/2~with~FCNC)}\\&\quad >\Gamma \mathrm{(the~transition~1/2\rightarrow 3/2~with~FCNC)}. \end{aligned}$$In the transition \(1/2\rightarrow 1/2\) and \(1/2\rightarrow 3/2\) with FCNC cases, the decay widths are very close to each other for \(l=e/\mu \) cases, while it is about one order of magnitude smaller for \(l=\tau \) case. This can be attributed to the much smaller phase space for \(l=\tau \) case.
A reasonable modification with momentum-space wave function \(\Psi ^{SS_{z}}\) in the case of an axial-vector diquark involved is performed in this work in Eqs. (2) and (3). While, in Refs. [8, 13, 22], the momentum-space wave function \(\Psi ^{SS_{z}}\) in the case of an axial-vector diquark involved is defined as
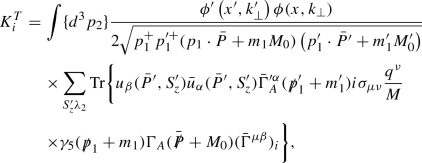 (116)
(116) (117)
(117)In Refs. [8] the extraction approach is different from the one used in this work and in Refs. [13, 22]. In order to find out the impact on the form factors and decay widths of these two factors: the extraction method of the form factors and the baryon wave function related to the axial vector diquark, we list numerical results of theses form factors of the three decay channels and the corresponding partial decay widths in Table 20. The corresponding numerical results in Refs. [8, 13, 22] are also given in Table 20.
Firstly, comparing each first two lines for \(\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}l^{+}\nu _{l}\), \(\Xi _{bb}^{0}\rightarrow \Xi _{b}^{0}e^{+}e^{-}\) and \(\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{*+}l^{+}\nu _{l}\), we could find that partial decay width differences coming from the different wave function with axial-vector diquark are small, but there are some differences among the form factors. Secondly, comparing the second line and third line of the channel \(\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}l^{+}\nu _{l}\), we could find the extracting approach of these form factors will bring in some effect in the form factors and decay widths; So the effect in the form factors and decay widths brought in by the extraction approach is much larger than that of the definition of the wave function \(\Psi ^{SS_{z}}\).
Since there exist uncertainties in the lifetimes of the parent baryons, there may be some small fluctuations in the results for branching ratios. From Table 17, we may find that
$$\begin{aligned} {{\mathcal {B}}}(\Xi ^{++}_{cc}\rightarrow \Xi ^{\prime +}_{c}l^{+}\nu _{l})= & {} 5.57\times 10^{-2},\nonumber \\ {{\mathcal {B}}}(\Xi ^{++}_{cc}\rightarrow \Xi ^{+}_{c}l^{+}\nu _{l})= & {} 3.40\times 10^{-2}, \end{aligned}$$(118)$$\begin{aligned} {{\mathcal {B}}}(\Omega ^{+}_{cc}\rightarrow \Omega ^{0}_{c}l^{+}\nu _{l})= & {} 7.67\times 10^{-2},\nonumber \\ {{\mathcal {B}}}(\Xi ^{+}_{bc}\rightarrow \Xi ^{\prime 0}_{b}l^{+}\nu _{l})= & {} 2.50\times 10^{-2}. \end{aligned}$$(119)These channels may be firstly examined at experimental facilities like LHC or BelleII.
Take the four processes \(\Xi ^{++}_{cc}\rightarrow \Lambda _{c}^{+}l^{+}\nu _{l}\), \(\Xi ^{++}_{cc}\rightarrow \Sigma _{c}^{*+}l^{+}\nu _{l}\), \(\Xi ^{0}_{bb}\rightarrow \Xi _{b}^{0}e^{+}e^{-}\) and \(\Xi ^{0}_{bb}\rightarrow \Xi _{b}^{\prime *0}e^{+}e^{-}\) as examples. The uncertainties for the partial decay widths caused by the model parameters and the single pole assumption for \(c\rightarrow d,s\) channels are listed as
$$\begin{aligned}&\Gamma \Big (\Xi ^{++}_{cc}\rightarrow \Lambda _{c}^{+}l^{+}\nu _{l}\Big )\nonumber \\&\quad =(7.97\pm 0.65\pm 1.28\pm 1.55\pm 1.65)\times 10^{-15}~\mathrm{GeV},\nonumber \\&\Gamma \Big (\Xi ^{++}_{cc}\rightarrow \Sigma _{c}^{*+}l^{+}\nu _{l}\Big )\nonumber \\&\quad =(1.43\pm 0.23\pm 0.29\pm 0.29\pm 0.16)\times 10^{-15}~\mathrm{GeV}, \nonumber \\ \end{aligned}$$(120)where these errors come from \(\beta _{i}\), \(\beta _{f}\), \(m_{\mathrm{di}}\) and \(m_{\mathrm{pole}}\) respectively;
$$\begin{aligned}&\Gamma \Big (\Xi ^{0}_{bb}\rightarrow \Xi _{b}^{0}e^{+}e^{-}\Big )\nonumber \\&\quad =(1.62\pm 0.69\pm 0.96\pm 0.17)\times 10^{-19}~\mathrm{GeV},\nonumber \\&\Gamma \Big (\Xi ^{0}_{bb}\rightarrow \Xi _{b}^{\prime *0}e^{+}e^{-}\Big )\nonumber \\&\quad =(1.45\pm 0.19\pm 0.70\pm 0.43)\times 10^{-19}~\mathrm{GeV}, \nonumber \\ \end{aligned}$$(121)where these errors come from \(\beta _{i}\), \(\beta _{f}\), \(m_{\mathrm{di}}\), respectively. Taking \(\Xi _{cc}^{++}\rightarrow \Lambda ^{+}_{c}\) as an example, the error estimates for the form factors can be found in Table 21.
It can be seen from Eqs. (120–121) and Table 21 that, the uncertainties caused by these parameters may be sizable.
The ratios \(\Gamma _{L}/\Gamma _{T}\)s have the following rule:
$$\begin{aligned}&c\rightarrow d:~\Gamma _{L}/\Gamma _{T}\Big (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}l^{+}\nu _{l}\Big )\nonumber \\&\quad = \Gamma _{L}/\Gamma _{T}\Big (\Xi _{cc}^{+}\rightarrow \Sigma _{c}^{0}l^{+}\nu _{l}\Big )\nonumber \\&\quad = \Gamma _{L}/\Gamma _{T}\Big (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}l^{+}\nu _{l}\Big ), \end{aligned}$$(122)$$\begin{aligned}&c\rightarrow s:~\Gamma _{L}/\Gamma _{T}\Big (\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime +}l^{+}\nu _{l}\Big )\nonumber \\&\quad = \Gamma _{L}/\Gamma _{T}\Big (\Xi _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}l^{+}\nu _{l}\Big )\nonumber \\&\quad = \Gamma _{L}/\Gamma _{T}\Big (\Omega _{cc}^{+}\rightarrow \Omega _{c}^{0}l^{+}\nu _{l}\Big ), \end{aligned}$$(123)for these decay channels in Eq. (122) have the same decay in quark level and the final single heavy baryons all in the sextets which leads to the same overlapping factors in the SU(3) symmetry. In other decay channels the similar relations exist. For the transition \(1/2\rightarrow 3/2\), we have the following relations:
$$\begin{aligned} \Gamma _{L}/\Gamma _{T}\Big (B_{bc}^{\prime }\rightarrow B_{b}^{*}l^{+}\nu _{l}\Big )= & {} \Gamma _{L}/\Gamma _{T}\Big (B_{bc}\rightarrow B_{b}^{*}l^{+}\nu _{l}\Big ), \nonumber \\ \end{aligned}$$(124)$$\begin{aligned} \Gamma _{L}/\Gamma _{T}\Big (B_{bc}^{\prime }\rightarrow B_{c}^{*}l^{-}{{{\bar{\nu }}}}_{l}\Big )= & {} \Gamma _{L}/\Gamma _{T}\Big (B_{bc}\rightarrow B_{c}^{*}l^{-}{{{\bar{\nu }}}}_{l}\Big ), \nonumber \\ \end{aligned}$$(125)$$\begin{aligned} \Gamma _{L}/\Gamma _{T}\Big (B_{bc}^{\prime }\rightarrow B_{c}^{*}l^{+}l^{-}\Big )= & {} \Gamma _{L}/\Gamma _{T}\Big (B_{bc}\rightarrow B_{c}^{*}l^{+}l^{-}\Big ), \nonumber \\ \end{aligned}$$(126)for these decay channels have the same decay in quark level and the spin of final single heavy baryons are all 3/2, only with the axial-vector diquark spectator which have the same overlapping factors and form factors. As shown in Figs. 9, 10, 11 and 12 and Tables 16, 17, 18 and 19, these decay channels with same \(\Gamma _{L}/\Gamma _{T}\) have the similar plots of the dependence of \(d\Gamma _{L}/dq^2\) and \(d\Gamma _{T}/dq^2\) on \(q^2\).
From Figs. 10 and 12 , it can be found that, at small \(q^2\), there are some divergence of the \(d\Gamma _{L}/dq^2\) and \(d\Gamma _{T}/dq^2\) for the cases \({{\mathcal {B}}}_{bb}\rightarrow {{\mathcal {B}}}_{b}^{(*)} e^{+}e^{-}/ \mu ^{+}\mu ^{-}\) and \({{\mathcal {B}}}_{bb}\rightarrow {{\mathcal {B}}}_{bc}^{(*)} l^{-}{{\bar{\nu }}}_{l}\), because \({1/\sqrt{q^2}}\) is included in their helicity amplitudes shown with Eqs. (83), (92), (96), (103), (105).
The differential decay widths \(d\Gamma _{L}/dq^2\) and \(d\Gamma _{T}/dq^2\) for the processes \({{\mathcal {B}}}_{bb}\rightarrow \mathcal{B}_{b}({{\mathcal {B}}}_{bc})l^-{{\bar{\nu }}}_{l}\) dependence on \(q^2\). Blue solid line: \(d\Gamma _{L}/dq^2\) defined with Eq. (80), red dashes line: \(d\Gamma _{T}/dq^2\) defined with Eq. (81)
The differential decay widths \(d\Gamma _{L}/dq^2\) and \(d\Gamma _{T}/dq^2\) for the processes \({{\mathcal {B}}}_{bb}\rightarrow \mathcal{B}_{b}l^+l^{-}\) dependence on \(q^2\). Blue solid line: \(d\Gamma _{L}/dq^2\) defined with Eq. (100), red dashes line: \(d\Gamma _{T}/dq^2\) defined with Eq. (101)
The differential decay widths \(d\Gamma _{L}/dq^2\) and \(d\Gamma _{T}/dq^2\) for the processes \({{\mathcal {B}}}_{bb}\rightarrow \mathcal{B}_{b}^{*}({{\mathcal {B}}}_{bc}^{*})l^-{{\bar{\nu }}}_{l}\) dependence on \(q^2\). Blue solid line: \(d\Gamma _{L}/dq^2\) defined with Eq. (88), red dashes line: \(d\Gamma _{T}/dq^2\) defined with Eq. (89)
The differential decay widths \(d\Gamma _{L}/dq^2\) and \(d\Gamma _{T}/dq^2\) for the processes \({{\mathcal {B}}}_{bb}\rightarrow \mathcal{B}_{b}^{*}l^+l^{-}\) dependence on \(q^2\). Blue solid line: \(d\Gamma _{L}/dq^2\) defined with Eq. (112), red dashes line: \(d\Gamma _{T}/dq^2\) defined with Eq. (113)
4.3 SU(3) symmetry for semileptonic decays
Recently, an analysis of weak decays of doubly heavy baryons based on flavor symmetry is available in Refs. [73, 74]. In the SU(3) symmetry limit, there exist the a number of relations among these semileptonic decay widths, which we are going to examine in the following.
For \(c\rightarrow d,s\) processes, we have
$$\begin{aligned} \Gamma \Big (\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}l^{+}\nu _{l}\Big )&=\Gamma \Big (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{0}l^{+}\nu _{l}\Big ),\\ \Gamma \Big (\Xi _{cc}^{++}\rightarrow \Xi _{c}^{+}l^{+}\nu _{l}\Big )&=\Gamma \Big (\Xi _{cc}^{+}\rightarrow \Xi _{c}^{0}l^{+}\nu _{l}\Big ),\\ \Gamma \Big (\Xi _{cc}^{+}\rightarrow \Sigma _{c}^{(*)0}l^{+}\nu _{l}\Big )&= 2\Gamma \Big (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{(*)+}l^{+}\nu _{l}\Big )\\&=2\Gamma \Big (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{\prime (*)0}l^{+}\nu _{l}\Big ),\\ \Gamma \Big (\Omega _{cc}^{+}\rightarrow \Omega _{c}^{(*)0}l^{+}\nu _{l}\Big )&=2\Gamma \Big (\Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime (*)+}l^{+}\nu _{l}\Big )\\&=2\Gamma \Big (\Xi _{cc}^{+}\rightarrow \Xi _{c}^{\prime (*)0}l^{+}\nu _{l}\Big ),\\ \Gamma \Big (\Xi _{bc}^{(\prime )+}\rightarrow \Lambda _{b}^{0}l^{+}\nu _{l}\Big )&=\Gamma \Big (\Omega _{bc}^{(\prime )0}\rightarrow \Xi _{b}^{-}l^{+}\nu _{l}\Big ),\\ \Gamma \Big (\Xi _{bc}^{(\prime )+}\rightarrow \Xi _{b}^{0}l^{+}\nu _{l}\Big )&=2\Gamma \Big (\Xi _{bc}^{(\prime )0}\rightarrow \Xi _{b}^{-}l^{+}\nu _{l}\Big ),\\ 2\Gamma \Big (\Xi _{bc}^{(\prime )+}\rightarrow \Sigma _{b}^{(*)0}l^{+}\nu _{l}\Big )&=\Gamma \Big (\Xi _{bc}^{(\prime )0}\rightarrow \Sigma _{b}^{(*)-}l^{+}\nu _{l}\Big )\\&=2\Gamma \Big (\Omega _{bc}^{(\prime )0}\rightarrow \Xi _{b}^{\prime (*)-}l^{+}\nu _{l}\Big ),\\ 2\Gamma \Big (\Xi _{bc}^{(\prime )+}\rightarrow \Xi _{b}^{\prime (*)0}l^{+}\nu _{l}\Big )&=2\Gamma \Big (\Xi _{bc}^{(\prime )0}\rightarrow \Xi _{b}^{\prime (*)-}l^{+}\nu _{l}\Big )\\&=\Gamma \Big (\Omega _{bc}^{(\prime )0}\rightarrow \Omega _{b}^{(*)-}l^{+}\nu _{l}\Big ). \end{aligned}$$For \(b\rightarrow u,c\) processes, we have
$$\begin{aligned} \Gamma \Big (\Xi _{bb}^{-}\rightarrow \Lambda _{b}^{0}l^{-}{{\bar{\nu }}}_{l}\Big )&=\Gamma \Big (\Omega _{bb}^{-}\rightarrow \Xi _{b}^{0}l^{-}{{\bar{\nu }}}_{l}\Big ),\\ \Gamma \Big (\Xi _{bb}^{0}\rightarrow \Xi _{bc}^{(*)+}l^{-}{{\bar{\nu }}}_{l}\Big )&= \Gamma \Big (\Xi _{bb}^{-}\rightarrow \Xi _{bc}^{(*)0}l^{-}{{\bar{\nu }}}_{l}\Big )\\&=\Gamma \Big (\Omega _{bb}^{-}\rightarrow \Omega _{bc}^{(*)0}l^{-}{{\bar{\nu }}}_{l}\Big ),\\ \Gamma \Big (\Xi _{bb}^{0}\rightarrow \Sigma _{b}^{(*)+}l^{-}{{\bar{\nu }}}_{l}\Big )&= 2\Gamma \Big (\Xi _{bb}^{-}\rightarrow \Sigma _{b}^{(*)0}l^{-}{{\bar{\nu }}}_{l})\\&=2\Gamma \Big (\Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime (*)0}l^{-}{{\bar{\nu }}}_{l}\Big ),\\ \Gamma \Big (\Xi _{bc}^{(\prime )+}\rightarrow \Xi _{cc}^{(*)++}l^{-}{{\bar{\nu }}}_{l}\Big )&= \Gamma \Big (\Xi _{bc}^{(\prime )0}\rightarrow \Xi _{cc}^{(*)+}l^{-}{{\bar{\nu }}}_{l}\Big )\\&=\Gamma \Big (\Omega _{bc}^{(\prime )0}\rightarrow \Omega _{cc}^{(*)+}l^{-}{{\bar{\nu }}}_{l}\Big ),\\ \Gamma \Big (\Xi _{bc}^{(\prime )+}\rightarrow \Sigma _{c}^{(*)++}l^{-}{{\bar{\nu }}}_{l}\Big )&=2\Gamma \Big (\Xi _{bc}^{(\prime )0}\rightarrow \Sigma _{c}^{(*)+}l^{-}{{\bar{\nu }}}_{l}\Big )\\&= 2\Gamma \Big (\Omega _{bc}^{(\prime )0}\rightarrow \Xi _{c}^{\prime (*)+}l^{-}{{\bar{\nu }}}_{l}\Big ). \end{aligned}$$
According to the flavor SU(3) symmetry, there exist the following relations among these FCNC processes. These relations can be readily derived using the overlapping factors given in Table 2.
For \(b\rightarrow d\) processes, we have
$$\begin{aligned} \Gamma \big (\Xi _{bb}^{0}\rightarrow \Lambda _{b}^{0}l^{+}l^{-}\big )= & {} \Gamma \big (\Omega _{bb}^{-}\rightarrow \Xi _{b}^{-}l^{+}l^{-}\big ), \\ 2\Gamma \big (\Xi _{bb}^{0}\rightarrow \Sigma _{b}^{(*)0}l^{+}l^{-}\big )= & {} \Gamma \big (\Xi _{bb}^{-}\rightarrow \Sigma _{b}^{(*)-}l^{+}l^{-}\big )\\= & {} 2\Gamma \big (\Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime (*)0}l^{+}l^{-}\big ),\\ \Gamma \big (\Xi _{bc}^{(\prime )+}\rightarrow \Lambda _{c}^{+}l^{+}l^{-}\big )= & {} \Gamma \big (\Omega _{bc}^{(\prime )0}\rightarrow \Xi _{c}^{0}l^{+}l^{-}\big ),\\ 2\Gamma \big (\Xi _{bc}^{(\prime )+}\rightarrow \Sigma _{c}^{(*)+}l^{+}l^{-}\big )= & {} \Gamma \big (\Xi _{bc}^{(\prime )0}\rightarrow \Sigma _{c}^{(*)0}l^{+}l^{-}\big )\\ \quad= & {} 2\Gamma \big (\Omega _{bc}^{(\prime )0}\rightarrow \Xi _{c}^{\prime (*)0}l^{+}l^{-}\big ). \end{aligned}$$For \(b\rightarrow s\) processes, we have
$$\begin{aligned} \Gamma \big (\Xi _{bb}^{0}\rightarrow \Xi _{b}^{0}l^{+}l^{-}\big )= & {} \Gamma \big (\Xi _{bb}^{-}\rightarrow \Xi _{b}^{-}l^{+}l^{-}\big ),\\ 2\Gamma \big (\Xi _{bb}^{0}\rightarrow \Xi _{b}^{\prime (*)0}l^{+}l^{-}\big )= & {} 2\Gamma \big (\Xi _{bb}^{-}\rightarrow \Xi _{b}^{\prime (*)-}l^{+}l^{-}\big )\\= & {} \Gamma \big (\Omega _{bb}^{-}\rightarrow \Omega _{b}^{(*)-}l^{+}l^{-}\big ),\\ \Gamma \big (\Xi _{bc}^{(\prime )+}\rightarrow \Xi _{c}^{+}l^{+}l^{-}\big )= & {} \Gamma \big (\Xi _{bc}^{(\prime )0}\rightarrow \Xi _{c}^{0}l^{+}l^{-}\big ),\\ 2\Gamma \big (\Xi _{bc}^{(\prime )+}\rightarrow \Xi _{c}^{\prime (*)+}l^{+}l^{-}\big )= & {} 2\Gamma \big (\Xi _{bc}^{(\prime )0}\rightarrow \Xi _{c}^{\prime (*)0}l^{+}l^{-}\big )\\= & {} \Gamma \big (\Omega _{bc}^{(\prime )0}\rightarrow \Omega _{c}^{(*)0}l^{+}l^{-}\big ). \end{aligned}$$
Comparing the above equations predicted by SU(3) symmetry with the corresponding results in this work, we have the following remarks:
most of our numerical results are respected very well with the SU(3) symmetry relations, except for the following ones
$$\begin{aligned} \Gamma \big (\Xi _{cc}^{++}\rightarrow \Lambda _{c}^{+}l^{+}\nu _{l}\big )&= \Gamma \big (\Omega _{cc}^{+}\rightarrow \Xi _{c}^{0}l^{+}\nu _{l}\big ),\nonumber \\ \Gamma \big (\Xi _{bc}^{+}\rightarrow \Lambda _{b}^{0}l^{+}\nu _{l}\big )&= \Gamma \big (\Omega _{bc}^{0}\rightarrow \Xi _{b}^{-}l^{+}\nu _{l}\big ),\nonumber \\ \Gamma \big (\Xi _{bc}^{+}\rightarrow \Sigma _{b}^{(*)0}l^{+}\nu _{l}\big )&= \Gamma \big (\Omega _{bc}^{0}\rightarrow \Xi _{b}^{\prime (*)-}l^{+}\nu _{l}\big ),\nonumber \\ \Gamma \big (\Xi _{bc}^{+}\rightarrow \Xi _{b}^{\prime (*)0}l^{+}\nu _{l}\big )&= \frac{1}{2}\Gamma \big (\Omega _{bc}^{0}\rightarrow \Omega _{b}^{(*)-}l^{+}\nu _{l}\big ),\nonumber \\ \Gamma \big (\Xi _{bc}^{0}\rightarrow \Sigma _{c}^{(*)+}l^{-}{{\bar{\nu }}}_{l}\big )&= \Gamma \big (\Omega _{bc}^{0}\rightarrow \Xi _{c}^{\prime (*)+}l^{-}{{\bar{\nu }}}_{l}\big ). \end{aligned}$$(127)These five relations are broken considerably: larger than 20% but still less than 50% using the definition of \((\mathrm{Max}[\Gamma _{\mathrm{LHS}},\Gamma _{\mathrm{RHS}}]-\mathrm{Min}[\Gamma _{\mathrm{LHS}},\Gamma _{\mathrm{RHS}}])/\mathrm{Max}[\Gamma _{\mathrm{LHS}},\Gamma _{\mathrm{RHS}}]\). Since the mass difference between the u and d quark has been neglected in this work, the isospin symmetry is well respected. But since the strange quark is much heavier, the SU(3) relations for the channels involving u, d quark and s quark can be significantly broken. All relations given in Eq. (127) are of this type.
The first four relations in Eq. (127) involve the c quark decay but the last one involves the b quark decay. It indicates that the c quark decay modes tend to break SU(3) symmetry easily. This can be understood since the phase space of the c quark decay is smaller, and thus the decay amplitude is more sensitive to the mass of the initial and final baryons.
SU(3) symmetry breaking is larger for the Qs diquark involved case than that for the Qu/Qd diquark involved case with \(Q=b,c\). SU(3) symmetry breaking is larger for the cq diquark involved case than that for the bq diquark involved case with \(q=u,d,s\).
SU(3) symmetry breaking is smaller for \(l=e/\mu \) cases than that for \(l=\tau \) case. This can be attributed to the much smaller phase space for \(l=\tau \) case. Smaller phase space is more sensitive to the variation of the masses of baryons in the initial and final states.
5 Conclusion
In this paper, we have presented a systematic investigation of transition form factors of doubly heavy baryon decays in the light front approach. Our main results for the form factors with the \(q^2\) distributions are collected in Tables 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16. The present analysis is the sequel and update of the previous works on weak decays of doubly heavy baryons, Refs. [8, 13, 22]. It improves upon the previous work by
adding predictions for the FCNC processes with the spin-1/2 to spin-3/2 transition;
using a new extraction of the Lorentz structure for the form factors;
updating the wave function for spin-1/2 baryons states with an axial-vector diquark ;
updating the wave function for spin-3/2 baryons states;
presenting a new derivation of the overlapping factors using flavor SU(3) symmetry approach;
presenting the momentum distribution of form factors.
Using these form factors, we have also preformed the calculation of phenomenological observables of these corresponding semileptonic weak decays of doubly heavy baryons with the results shown in Tables 16, 17, 18 and 19. The flavor SU(3) symmetry and sources of symmetry breaking are also discussed in great details. We find that,
most branching ratios for spin-1/2 to spin-1/2 with \(c\rightarrow d,s\) processes are at the order \(10^{-3}{-}10^{-2}\), which might be examined at experimental facilities at LHC or Belle-II;
the different extraction approaches could give sizable differences to form factors;
the uncertainties of form factors and decay widths caused by model parameters are sizable;
the ratios \(\Gamma _{L}/\Gamma _{T}\)s have the rules shown in Eqs. (122)–(126), for these decay channels have the same decay in quark level and the same overlapping factors and form factors;
most of our results are comparable to the theoretical results in Refs. [8, 13, 22];
since the mass difference between the u and d quark has been neglected and the strange quark is much heavier, the SU(3) relations shown in Eq. (127) for the channels involving u, d quark and s quark can be broken;
the SU(3) symmetry breaking is sizable in the charmed baryon decays, while for the bottomed case the SU(3) symmetry breaking is small.
This work completes the study of form factors in the traditional LFQM with the quark-diquark constituent viewpoint. We hope our phenomenology predictions for these semi-leptonic decays could be tested by LHCb and other experiments in the future.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study and no experimental data has been listed.]
Notes
In the following, we will abbreviate the spin-\(S_1\) to spin-\(S_2\) transition as the \(S_1\rightarrow S_2\) transition. If there is no special note, spin-1/2 and spin-3/2 are all with positive parity. We will omit the positive sign of positive parity in the following.
References
R. Aaij et al. [LHCb Collaboration], Phys. Rev. Lett. 119(11), 112001 (2017). https://doi.org/10.1103/PhysRevLett.119.112001. arXiv:1707.01621 [hep-ex]
F.S. Yu, H.Y. Jiang, R.H. Li, C.D.L, W. Wang , Z.X. Zhao, Chin. Phys. C 42(5), 051001 (2018). https://doi.org/10.1088/1674-1137/42/5/051001. arXiv:1703.09086 [hep-ph]
R. Aaij et al. [LHCb Collaboration], Phys. Rev. Lett. 121(16), 162002 (2018). https://doi.org/10.1103/PhysRevLett.121.162002. arXiv:1807.01919 [hep-ex]
R. Aaij et al. [LHCb Collaboration], Phys. Rev. Lett. 121(5), 052002 (2018). https://doi.org/10.1103/PhysRevLett.121.052002. arXiv:1806.02744 [hep-ex]
R. Aaij et al. [LHCb Collaboration], Sci. China Phys. Mech. Astron. 63(2), 221062 (2020). https://doi.org/10.1007/s11433-019-1471-8. arXiv:1909.12273 [hep-ex]
R. Aaij et al. [LHCb Collaboration], JHEP 1910, 124 (2019). https://doi.org/10.1007/JHEP10(2019)124. arXiv:1905.02421 [hep-ex]
R. Aaij et al. [LHCb Collaboration]. arXiv:1911.08594 [hep-ex]
W. Wang, F.S. Yu, Z.X. Zhao, Eur. Phys. J. C 77(11), 781 (2017). https://doi.org/10.1140/epjc/s10052-017-5360-1. arXiv:1707.02834 [hep-ph]
X.H. Hu, Y.L. Shen, W. Wang, Z.X. Zhao, Chin. Phys. C 42(12), 123102 (2018). https://doi.org/10.1088/1674-1137/42/12/123102. arXiv:1711.10289 [hep-ph]
T. Gutsche, M.A. Ivanov, J.G. Krner, V.E. Lyubovitskij, Phys. Rev. D 96(5), 054013 (2017). https://doi.org/10.1103/PhysRevD.96.054013. arXiv:1708.00703 [hep-ph]
N. Sharma, R. Dhir, Phys. Rev. D 96(11), 113006 (2017). https://doi.org/10.1103/PhysRevD.96.113006. arXiv:1709.08217 [hep-ph]
Z.X. Zhao, Chin. Phys. C 42(9), 093101 (2018). https://doi.org/10.1088/1674-1137/42/9/093101. arXiv:1803.02292 [hep-ph]
Z.X. Zhao, Eur. Phys. J. C 78(9), 756 (2018). https://doi.org/10.1140/epjc/s10052-018-6213-2. arXiv:1805.10878 [hep-ph]
F.S. Yu, Sci. China Phys. Mech. Astron. 63, 221065 (2020). https://doi.org/10.1007/s11433-019-1483-0. arXiv:1912.10253 [hep-ex]
T. Gutsche, M.A. Ivanov, J.G. Krner, V.E. Lyubovitskij, Z. Tyulemissov, Phys. Rev. D 100(11), 114037 (2019). https://doi.org/10.1103/PhysRevD.100.114037. arXiv:1911.10785 [hep-ph]
A.I. Onishchenko. arXiv:hep-ph/0006295
D. Ebert, R.N. Faustov, V.O. Galkin , A.P. Martynenko, Phys. Rev. D 70, 014018 (2004). https://doi.org/10.1103/PhysRevD.70.014018, https://doi.org/10.1103/PhysRevD.77.079903. arXiv:hep-ph/0404280 [Erratum: [Phys. Rev. D 77, 079903 (2008)]
D. Ebert, R.N. Faustov, V.O. Galkin, A.P. Martynenko, Phys. Atom. Nucl. 68, 784 (2005). https://doi.org/10.1134/1.1935012. [Yad. Fiz.1538 68, 817 (2005)]
C. Albertus, E. Hernandez, J. Nieves, J.M. Verde-Velasco, Eur. Phys. J. A 31, 691 (2007). https://doi.org/10.1140/epja/i2006-10242-2. arXiv:hep-ph/0610131
C. Albertus, E. Hernandez, J. Nieves, Phys. Rev. D 85, 094035 (2012). https://doi.org/10.1103/PhysRevD.85.094035. arXiv:1202.4861 [hep-ph]
R. Dhir, N. Sharma, Eur. Phys. J. C 78(9), 743 (2018). https://doi.org/10.1140/epjc/s10052-018-6220-3
Z.P. Xing, Z.X. Zhao, Phys. Rev. D 98(5), 056002 (2018). https://doi.org/10.1103/PhysRevD.98.056002. arXiv:1807.03101 [hep-ph]
Q.A. Zhang, Eur. Phys. J. C 78(12), 1024 (2018). https://doi.org/10.1140/epjc/s10052-018-6481-x. arXiv:1811.02199 [hep-ph]
L.J. Jiang, B. He, R.H. Li, Eur. Phys. J. C 78(11), 961 (2018). https://doi.org/10.1140/epjc/s10052-018-6445-1. arXiv:1810.00541 [hep-ph]
H.W. Ke, F. Lu, X.H. Liu, X.Q. Li. arXiv:1912.01435 [hep-ph]
Y.J. Shi, W. Wang, Z.X. Zhao. arXiv:1902.01092 [hep-ph]
Y.J. Shi, Y. Xing, Z.X. Zhao, Eur. Phys. J. C 79(6), 501 (2019). https://doi.org/10.1140/epjc/s10052-019-7014-y. arXiv:1903.03921 [hep-ph]
X.H. Hu, Y.J. Shi, Eur. Phys. J. C 80(1), 56 (2020). https://doi.org/10.1140/epjc/s10052-020-7635-1. arXiv:1910.07909 [hep-ph]
A.S. Gerasimov, A.V. Luchinsky, Phys. Rev. D 100(7), 073015 (2019). https://doi.org/10.1103/PhysRevD.100.073015. arXiv:1905.11740 [hep-ph]
W. Jaus, Phys. Rev. D 60, 054026 (1999). https://doi.org/10.1103/PhysRevD.60.054026
W. Jaus, Phys. Rev. D 41, 3394 (1990). https://doi.org/10.1103/PhysRevD.41.3394
W. Jaus, Phys. Rev. D 44, 2851 (1991). https://doi.org/10.1103/PhysRevD.44.2851
H.Y. Cheng, C.Y. Cheung, C.W. Hwang, Phys. Rev. D 55, 1559 (1997). https://doi.org/10.1103/PhysRevD.55.1559. arXiv:hep-ph/9607332
H.Y. Cheng, C.K. Chua, C.W. Hwang, Phys. Rev. D 69, 074025 (2004). https://doi.org/10.1103/PhysRevD.69.074025. arXiv:hep-ph/0310359
H.Y. Cheng, C.K. Chua, Phys. Rev. D 69, 094007 (2004). https://doi.org/10.1103/PhysRevD.69.094007, https://doi.org/10.1103/PhysRevD.81.059901. arXiv:hep-ph/0401141 [Erratum: Phys. Rev. D 81, 059901 (2010)]
H.W. Ke, X.Q. Li, Z.T. Wei, Phys. Rev. D 80, 074030 (2009). https://doi.org/10.1103/PhysRevD.80.074030. arXiv:0907.5465 [hep-ph]
H.W. Ke, X.Q. Li, Z.T. Wei, Eur. Phys. J. C 69, 133 (2010). https://doi.org/10.1140/epjc/s10052-010-1383-6. arXiv:0912.4094 [hep-ph]
H.Y. Cheng, C.K. Chua, Phys. Rev. D 81, 114006 (2010). https://doi.org/10.1103/PhysRevD.81.114006, https://doi.org/10.1103/PhysRevD.82.059904. arXiv:0909.4627 [hep-ph] [Erratum: Phys. Rev. D 82, 059904 (2010)]
C.D. Lu, W. Wang, Z.T. Wei, Phys. Rev. D 76, 014013 (2007). https://doi.org/10.1103/PhysRevD.76.014013. arXiv:hep-ph/0701265 [HEP-PH]
W. Wang, Y.L. Shen, C.D. Lu, Eur. Phys. J. C 51, 841 (2007). https://doi.org/10.1140/epjc/s10052-007-0334-3. arXiv:0704.2493 [hep-ph]
W. Wang, Y.L. Shen, C.D. Lu, Phys. Rev. D 79, 054012 (2009). https://doi.org/10.1103/PhysRevD.79.054012. arXiv:0811.3748 [hep-ph]
W. Wang, Y.L. Shen, Phys. Rev. D 78, 054002 (2008). https://doi.org/10.1103/PhysRevD.78.054002
X.X. Wang, W. Wang, C.D. Lu, Phys. Rev. D 79, 114018 (2009). https://doi.org/10.1103/PhysRevD.79.114018. arXiv:0901.1934 [hep-ph]
C.H. Chen, Y.L. Shen, W. Wang, Phys. Lett. B 686, 118 (2010). https://doi.org/10.1016/j.physletb.2010.02.056. arXiv:0911.2875 [hep-ph]
G. Li, Fl Shao, W. Wang, Phys. Rev. D 82, 094031 (2010). https://doi.org/10.1103/PhysRevD.82.094031. arXiv:1008.3696 [hep-ph]
R.C. Verma, J. Phys. G 39, 025005 (2012). https://doi.org/10.1088/0954-3899/39/2/025005. arXiv:1103.2973 [hep-ph]
Y.J. Shi, W. Wang, Z.X. Zhao, Eur. Phys. J. C 76(10), 555 (2016). https://doi.org/10.1140/epjc/s10052-016-4405-1. arXiv:1607.00622 [hep-ph]
Q. Chang, X.N. Li, L.T. Wang, Eur. Phys. J. C 79(5), 422 (2019). https://doi.org/10.1140/epjc/s10052-019-6949-3. arXiv:1905.05098 [hep-ph]
Q. Chang, L.T. Wang, X.N. Li, JHEP 1912, 102 (2019). https://doi.org/10.1007/JHEP12(2019)102. arXiv:1908.04677 [hep-ph]
H.W. Ke, X.Q. Li, Z.T. Wei, Phys. Rev. D 77, 014020 (2008). https://doi.org/10.1103/PhysRevD.77.014020. arXiv:0710.1927 [hep-ph]
Z.T. Wei, H.W. Ke, X.Q. Li, Phys. Rev. D 80, 094016 (2009). https://doi.org/10.1103/PhysRevD.80.094016. arXiv:0909.0100 [hep-ph]
H.W. Ke, X.H. Yuan, X.Q. Li, Z.T. Wei, Y.X. Zhang, Phys. Rev. D 86, 114005 (2012). https://doi.org/10.1103/PhysRevD.86.114005. arXiv:1207.3477 [hep-ph]
J. Zhu, Z.T. Wei, H.W. Ke, Phys. Rev. D 99(5), 054020 (2019). https://doi.org/10.1103/PhysRevD.99.054020. arXiv:1803.01297 [hep-ph]
H.W. Ke, N. Hao, X.Q. Li, J. Phys. G 46(11), 115003 (2019). https://doi.org/10.1088/1361-6471/ab29a7. arXiv:1711.02518 [hep-ph]
C.K. Chua, Phys. Rev. D 99(1), 014023 (2019). https://doi.org/10.1103/PhysRevD.99.014023. arXiv:1811.09265 [hep-ph]
C.K. Chua, Phys. Rev. D 100(3), 034025 (2019). https://doi.org/10.1103/PhysRevD.100.034025. arXiv:1905.00153 [hep-ph]
T. Moroi. arXiv:hep-ph/9503210
Z.S. Brown, W. Detmold, S. Meinel, K. Orginos, Phys. Rev. D 90(9), 094507 (2014). https://doi.org/10.1103/PhysRevD.90.094507. arXiv:1409.0497 [hep-lat]
H.Y. Cheng, Y.L. Shi, Phys. Rev. D 98(11), 113005 (2018). https://doi.org/10.1103/PhysRevD.98.113005. arXiv:1809.08102 [hep-ph]
M. Karliner, J.L. Rosner, Phys. Rev. D 90(9), 094007 (2014). https://doi.org/10.1103/PhysRevD.90.094007. arXiv:1408.5877 [hep-ph]
V.V. Kiselev, A.K. Likhoded, Phys. Usp. 45, 455 (2002). https://doi.org/10.1070/PU2002v045n05ABEH000958. arXiv:hep-ph/0103169 [Usp. Fiz. Nauk 172, 497 (2002)]
V.V. Kiselev, A.K. Likhoded, Usp. Fiz. Nauk 172, 497 (2002). https://doi.org/10.1070/PU2002v045n05ABEH000958. arXiv:hep-ph/0103169
C. Patrignani et al. [Particle Data Group], Chin. Phys. C 40(10), 100001 (2016). https://doi.org/10.1088/1674-1137/40/10/100001
W. Jaus, D. Wyler, Phys. Rev. D 41, 3405 (1990). https://doi.org/10.1103/PhysRevD.41.3405
W. Jaus, Phys. Rev. D 53, 1349 (1996). https://doi.org/10.1103/PhysRevD.53.1349, https://doi.org/10.1103/PhysRevD.54.5904.2[Erratum: Phys. Rev. D 54, 5904 (1996)]
H.W. Ke, N. Hao, X.Q. Li, Eur. Phys. J. C 79(6), 540 (2019). https://doi.org/10.1140/epjc/s10052-019-7048-1. arXiv:1904.05705 [hep-ph]
M. Tanabashi et al. [Particle Data Group], Phys. Rev. D 98(3), 030001 (2018). https://doi.org/10.1103/PhysRevD.98.030001
G. Buchalla, A.J. Buras, M.E. Lautenbacher, Rev. Mod. Phys. 68, 1125 (1996). https://doi.org/10.1103/RevModPhys.68.1125. arXiv:hep-ph/9512380
R.H. Li, C.D. Lu, W. Wang, Phys. Rev. D 79, 094024 (2009). https://doi.org/10.1103/PhysRevD.79.094024. arXiv:0902.3291 [hep-ph]
C.D. Lu, W. Wang, Phys. Rev. D 85, 034014 (2012). https://doi.org/10.1103/PhysRevD.85.034014. arXiv:1111.1513 [hep-ph]
A.K. Giri, R. Mohanta, Eur. Phys. J. C 45, 151 (2006). https://doi.org/10.1140/epjc/s2005-02407-6. arXiv:hep-ph/0510171
A.J. Buras, M. Munz, Phys. Rev. D 52, 186 (1995). https://doi.org/10.1103/PhysRevD.52.186. arXiv:hep-ph/9501281
W. Wang, Z.P. Xing, J. Xu, Eur. Phys. J. C 77(11), 800 (2017). https://doi.org/10.1140/epjc/s10052-017-5363-y. arXiv:1707.06570 [hep-ph]
Y.J. Shi, W. Wang, Y. Xing, J. Xu, Eur. Phys. J. C 78(1), 56 (2018). https://doi.org/10.1140/epjc/s10052-018-5532-7. arXiv:1712.03830 [hep-ph]
L.L. Chau, H.Y. Cheng, B. Tseng, Phys. Rev. D 54, 2132 (1996). https://doi.org/10.1103/PhysRevD.54.2132. arXiv:hep-ph/9508382
Acknowledgements
We thank Prof. Wei Wang, Fu-Sheng Yu and Zhen-Xing Zhao for fruitful discussions. This work is supported in part by National Natural Science Foundation of China under Grants Nos. 11735010, 11911530088, and 11765012, Natural Science Foundation of Shanghai under Grants No. 15DZ2272100, and by Key Laboratory for Particle Physics, Astrophysics and Cosmology, Ministry of Education.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Wave functions in initial and final states
1.1 A1. Wave functions in the standard flavor-spin basis
The wave functions in the flavor space can also be found in Ref. [75]. The wave functions of the doubly heavy baryons in the standard flavor-spin basis are given as follows.
For \({{\mathcal {B}}}_{QQq}\) (\(\Xi _{cc}^{++,+}\), \(\Omega _{cc}^{+}\), \(\Xi _{bb}^{0,-}\) and \(\Omega _{bb}^{-}\)), their flavor-spin functions are given as
with \(q=u,d,s\) and \(Q=c,b\).
For the baryons with two different heavy quarks \({{\mathcal {B}}}_{Q_{1}Q_{2}q}\) ( \(\Xi _{bc}^{+,0}\) and \(\Omega _{bc}^{0}\)), their flavor-spin functions can be given as
where the two different heavy quarks are symmetry. While for the two different heavy quarks in baryons are anti-symmetry, the flavor-spin functions of these baryons \({{\mathcal {B}}}^{\prime }_{Q_{1}Q_{2}q}\) (\(\Xi _{bc}^{\prime +}\), \(\Xi _{bc}^{\prime 0}\) and \(\Omega _{bc}^{\prime 0}\)) are
where \(q=u,d,s\), \(Q_{1}=b\) and \(Q_{2}=c\).
are given with the following functions.
The flavor-spin wave functions of \({{\mathcal {B}}}_{Qqq}^{{\varvec{6}}}\) (\(\Sigma _{c}^{++,0}\), \(\Omega _{c}^{0}\), \(\Sigma _{b}^{+,-}\) and \(\Omega _{b}^{-}\)) are
where \(q=u,d,s\) and \(Q=c,b\).
When the two light quarks in the baryons \({{\mathcal {B}}}_{Qq_{1}q_{2}}^{{\varvec{6}}}\) (\(\Sigma _{c}^{+}\), \(\Xi _{c}^{\prime +,\prime 0}\), \(\Sigma _{b}^{0}\) and \(\Xi _{b}^{\prime 0,\prime -}\)) are different and symmetry, their flavor-spin wave functions are
with \((q_{1},q_{2})=(u,d),(u,s),(d,s)\) and \(Q=c,b\). While for the two different light quarks in baryons are anti-symmetry, the flavor-spin functions of these baryons \({{\mathcal {B}}}_{Qq_{1}q_{2}}^{\bar{{\varvec{3}}}}\) (\(\Lambda _{c}^{+}\), \(\Xi _{c}^{+,0}\), \(\Lambda _{b}^{0}\) and \(\Xi _{b}^{0,-}\)) are
with \((q_{1},q_{2})=(u,d),(u,s),(d,s)\) and \(Q=c,b\).
1.2 A2. Wave functions in the diquark basis
As we know, the coupling of the two angular momenta \(j_{1}=1\) and \(j_{2}=\frac{1}{2}\) is
Then the baryon state with an axial-vector diquark could be defined as follows,
with \((q_{2}q_{3})_{11}=(q_{2}q_{3})(\uparrow \uparrow )\) and \((q_{2}q_{3})_{10}=(q_{2}q_{3})\left( \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow )\right) \). For the baryon state with a scalar diquark, we have the following definition
with \((q_{2}q_{3})_{S}=(q_{2}q_{3})_{00}=(q_{2}q_{3})\left( \frac{1}{\sqrt{2}}(\uparrow \downarrow -\downarrow \uparrow )\right) \).
Using the above definitions, the following two equations can be proved
Then in the diquark basis, the flavor-spin wave functions of the initial and final baryon states can be derived with the help of above expressions and are shown in Sect. 2.2.
Appendix B: Helicity amplitude
The helicity amplitude of the decays in this work are derived from the effective Hamilton of semi-leptonic decays. Here we take the process \(c\rightarrow s l^{+}\nu _{l}\) as an example to derive the helicity amplitude. Firstly, the effective Hamilton of the process \(c\rightarrow s l^{+}\nu _{l}\) is
Secondly, the amplitude of the decay \(\Xi _{cc}^{++}\rightarrow \Xi _{c}^{+} l^{+}\nu _{l}\) can be written as
Here W can be regarded as a virtual propagation, and we use \(g_{\mu \nu }=\varepsilon ^*_{\mu }(t)\varepsilon _{\nu }(t) -\sum _{\lambda }\varepsilon ^*_{\mu }(\lambda )\varepsilon _{\nu }(\lambda )\) in deriving the last line the above equations.
Then the the hadronic helicity amplitude can be defined as
While the leptonic part amplitude can be calculated by the follow equation,

In this work, the dynamics involved in the the hadronic amplitude are all in the rest frame of the initial states \({{\mathcal {B}}}_{i}\),
While the dynamics involved in the the leptonic part are all in the rest frame of the virtual vector particle W. The spinor expressions involved in this work are given as follows:
here \(\lambda \) denotes the helicity of the spinor and (\(\theta \),\(\phi \)) are the direction of the momentum of the initial and final particles. In this work, we take the direction of the momentum of virtual vector particle W as positive with \((\theta ,\phi )=(0,0)\) and the direction of the momentum of the final baryons as negative direction with \((\theta ,\phi )=(\pi ,\pi )\), which are shown in Fig. 8.
The spinor expressions of anti-particles in the leptonic part are
In this work, the direction of the momentum of \(l^+\) is \((\theta _l,\phi _{l})\), and the direction of the momentum of \(\nu \) is \((\pi -\theta _l,\phi _{l}+\pi )\).
The hadronic helicity amplitude of the transition \({{\mathcal {B}}}_{QQ^{\prime }}(P,S=1/2)\rightarrow {{\mathcal {B}}}_{Q^{\prime }}^{*}(P^{\prime },S^{\prime }=3/2)\) can be get in a similar way with \({{\mathcal {B}}}_{QQ^{\prime }}(P,S=1/2)\rightarrow {{\mathcal {B}}}_{Q^{\prime }}^{*}(P^{\prime },S^{\prime }=1/2)\) shown by Eqs. (B2) and (B3). But the spinor for the final baryon \({{\mathcal {B}}}_{Q^{\prime }}^{*}(P^{\prime },S^{\prime }=3/2)\) is a vectorial spinor \(u_\alpha (P^{\prime },S^{\prime }=3/2)\) which is the coupling of one spinor \(u(P^{\prime },s_{1}=1/2)\) and a polarization vector \(\varepsilon (P^{\prime },s_{2}=1)\) and the detail coupling formula are given as follows,
with
Appendix C: Overlapping factors in flavor SU(3) symmetry
The overlapping factors can also be calculated using the flavor SU(3) symmetry. The doubly heavy baryons triplets are given as
and the singly heavy baryons anti-triplets are
the singly heavy baryons sextets are
For \({{\mathcal {B}}}_{cc}\rightarrow {{\mathcal {B}}}_{c}\) transitions with \(c\rightarrow u,d,s\), the SU(3) amplitude could be written as:
For \({{\mathcal {B}}}_{bc}\rightarrow {{\mathcal {B}}}_{b}\) transitions with \(c\rightarrow u,d,s\), it is:
For \({{\mathcal {B}}}_{bc}^{\prime }\rightarrow {{\mathcal {B}}}_{b}\) transitions with \(c\rightarrow u,d,s\), the amplitude is
For \({{\mathcal {B}}}_{bb}\rightarrow {{\mathcal {B}}}_{b}\) transitions with \(b\rightarrow u,d,s\), it is
The \({{\mathcal {B}}}_{bc}\rightarrow {{\mathcal {B}}}_{c}\) transitions with \(b\rightarrow u,d,s\) have the results
For \({{\mathcal {B}}}_{bc}^{\prime }\rightarrow {{\mathcal {B}}}_{c}\) transitions with \(b\rightarrow u,d,s\), the amplitude is:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Hu, XH., Li, RH. & Xing, ZP. A comprehensive analysis of weak transition form factors for doubly heavy baryons in the light front approach. Eur. Phys. J. C 80, 320 (2020). https://doi.org/10.1140/epjc/s10052-020-7851-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-7851-8